PN结仿真实例:半导体漂移扩散Drift-Diffusion
我们知道,导电的是载流子,包括空洞和电子。PN结中的P和N都是半导体材料,比如硅或锗,区别是用了不同的原子掺杂(doping)。若不掺杂,半导体硅本身的空洞或电子浓度就叫本征载流子浓度(intrinsiccarrier concentration),用Ni表示,与温度强相关;比如300开尔文的硅Ni约为10e9cm^-3,空洞和电子都是这个浓度,因为没有掺杂。掺杂多空洞载流子,硅便成了P类硅(P-type),掺杂多电子载流子,硅便成了N类硅(N-type)。P-type是受体acceptor,N-type是施体donor,所以N-type会贡献多余的电子给P-type,直到电势平衡,不再有载流子流动,这个过程就叫做扩散(diffusion)。当半导体中的载流子分布处于不平衡时,漂移扩散就会发生。比如半导体两端有电势差,或者半导体一部分有光照产生了多余载流子,都是载流子分布不平衡;
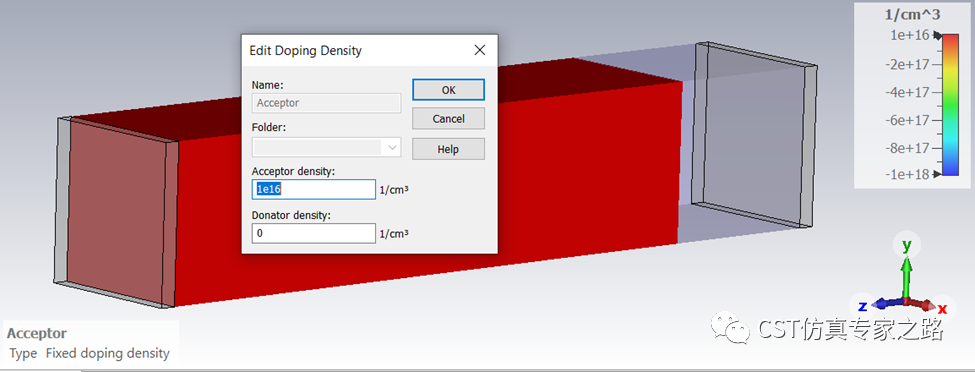
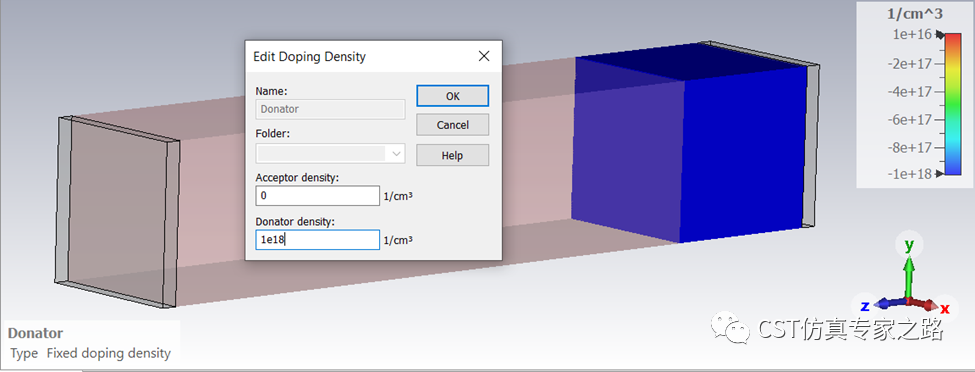
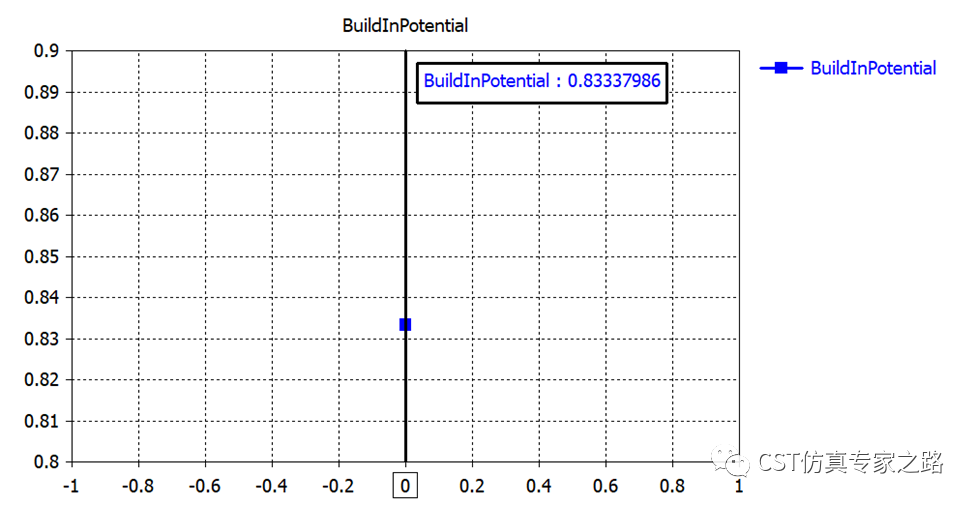
本案例中,P-type的掺杂密度为 NA=1e16 cm^-3, N-type的掺杂密度为ND=1e18cm^-3, 硅Ni=1e10cm^-3,有了这些输入值,加上室温热电压常数Vth=0.026mV,我们就可以手动计算出PN结中的内置电位(builtin potential):

漂移扩散求解器简称DD-solver,是低频工作室中求解器之一:
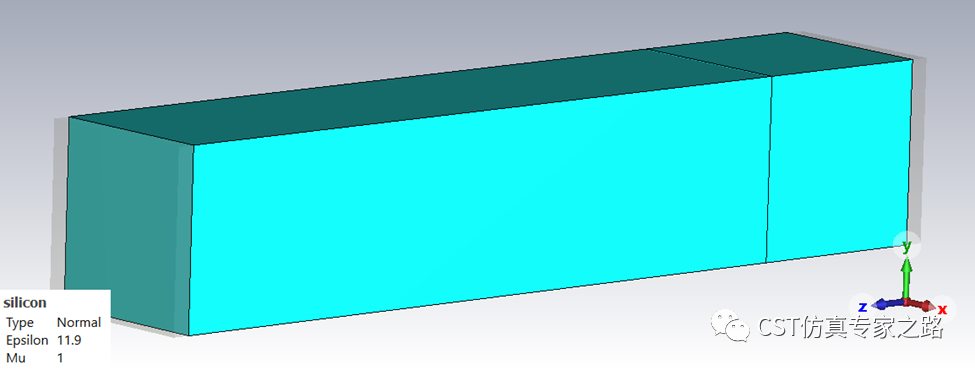
模型很简单,两个方块,都是硅材料,长度为0.4um和0.1um,XY方向较小,模拟一维结构。
特别的是,针对DD求解器,硅材料的设置中多了半导体相关的参数:
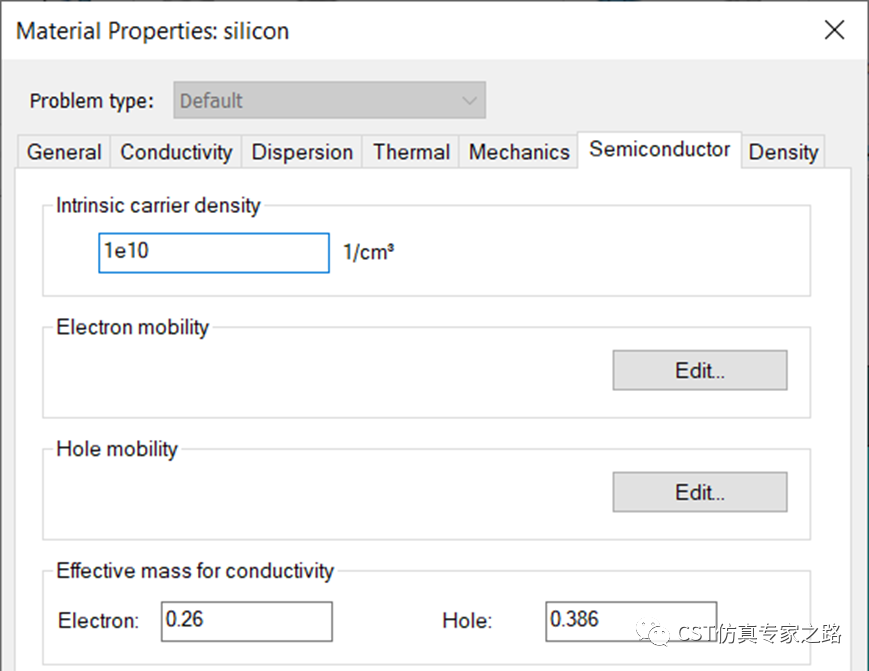
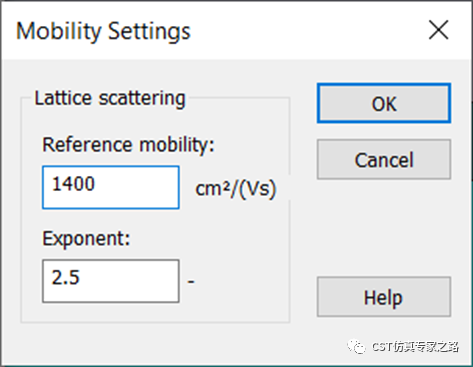
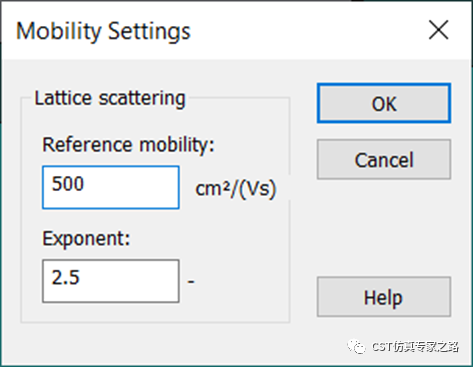
所以DD求解器需要材料中多明确本征载流子密度、载流子迁移率和载流子有效质量,这三大半导体材料参数。
其中,本征载流子密度容易理解,就是硅的特性;载流子迁移率乘以电场能获得漂移速度;
载流子有效质量是相对于自由电子的质量,一般都在范围0.01-10;可能有人问了,怎么空穴和电子的质量还能比电子小呢?这个就是固体物理的范畴了,需要具体的能级曲线分析,这里就不详细说了。
总之这些设置的值在很多文献或课本中都能找到。
具体的半导体掺杂则需要在Doping Density处设置:

P-type正掺杂:
N-type负掺杂:
两边用PEC添加固定电势,N-type一边是0电势的地,P-type一边是参数化的电压偏置,所以Voltage为正就是正向偏置,PN结导通;Voltage为负就是逆向偏置,PN结不通:


本地网格加密,N-type更密一些,因为他的掺杂是P-type的100倍,德拜长度就是P-type的1/10;德拜长度计算:
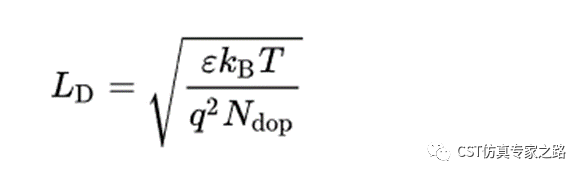
LD(donor)= sqrt(11.9*8.854e-12*1.3806e-23*300/1.6^2e-38/1e18/1e6) =4nm
LD(acceptor) = 40nm
所以大概一个德拜长度一个网格:
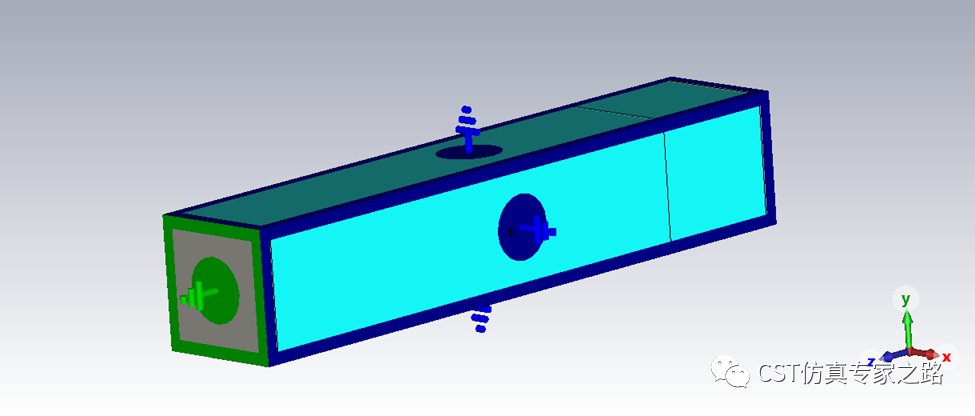
边界条件:

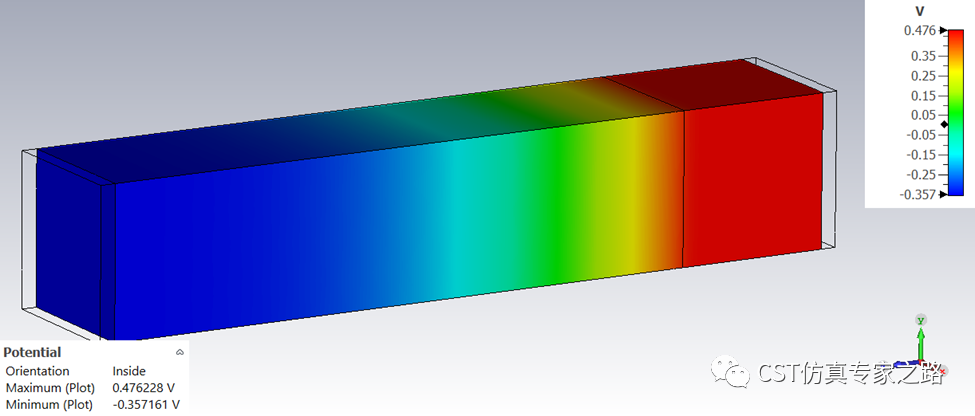
我们先用Voltage=0,也就是无外界偏置电压仿真,此时内置电压等于势垒电压。
仿真结束后,很多结果自动得到:
比如我们先查看载流子密度,两端最大值就是我们之前设置的掺杂密度;中间有耗尽区生成,所以P-type这边明显耗尽层较大,因为本案例P掺杂较少,这也是为什么我们画P长过N。实际中二极管往往P-type要短一些,和掺杂浓度有关。
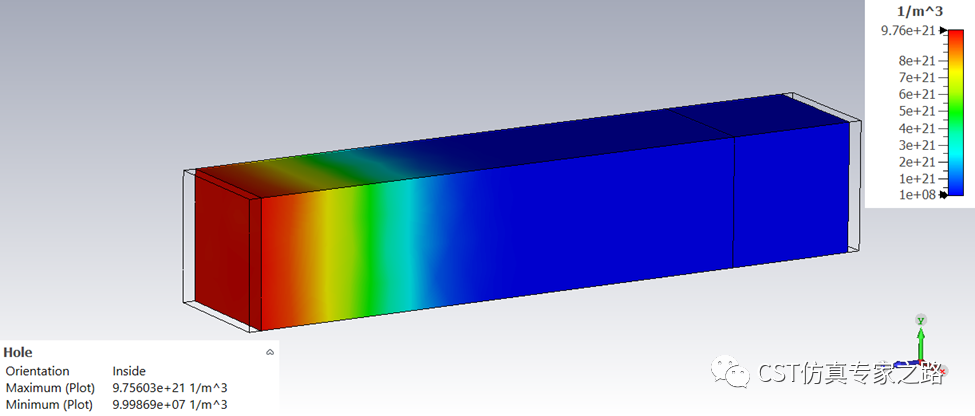
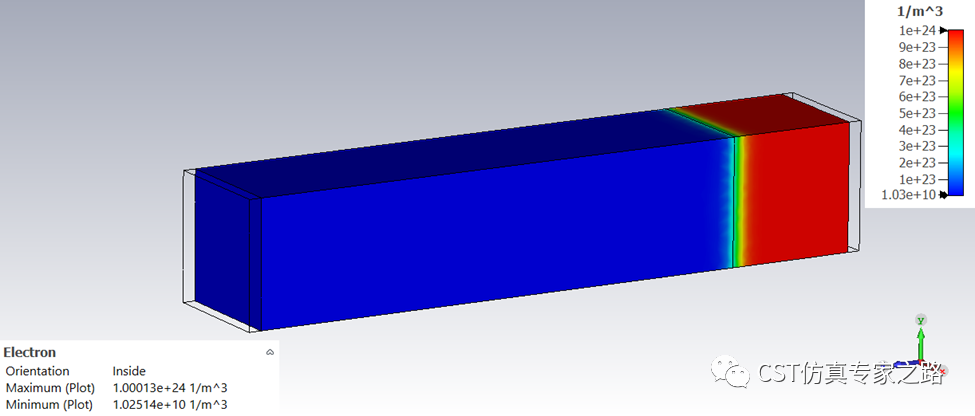
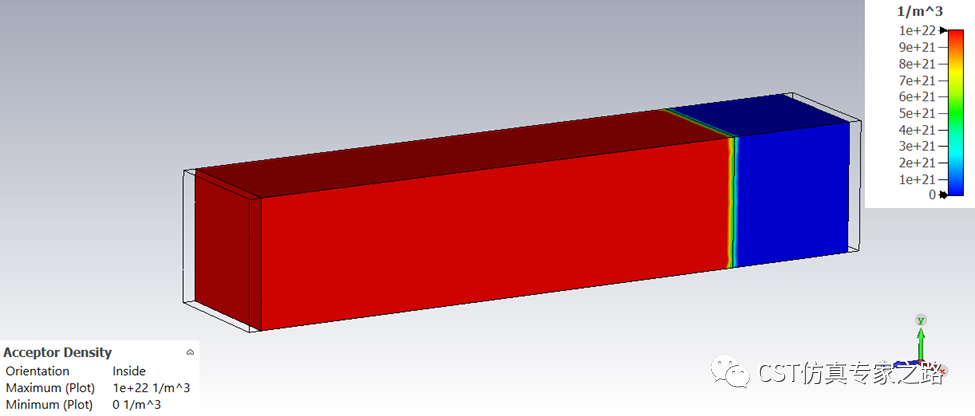
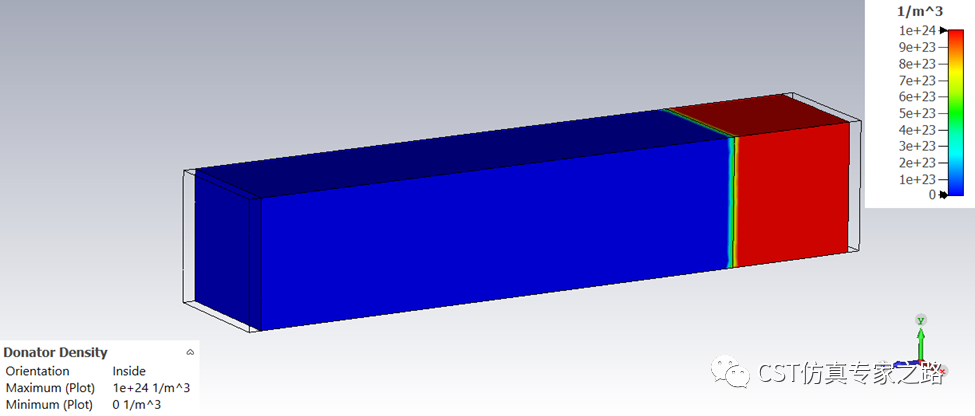
若看参杂密度,则是设置的定值:
电场分布:

电势分布:
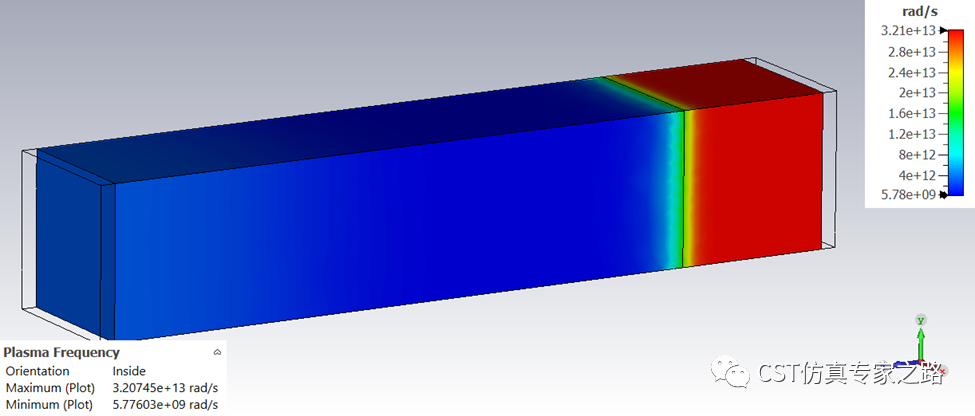
等离子频率:
我们用后处理提取中轴线上的电场、电势、电子密度、空穴密度:
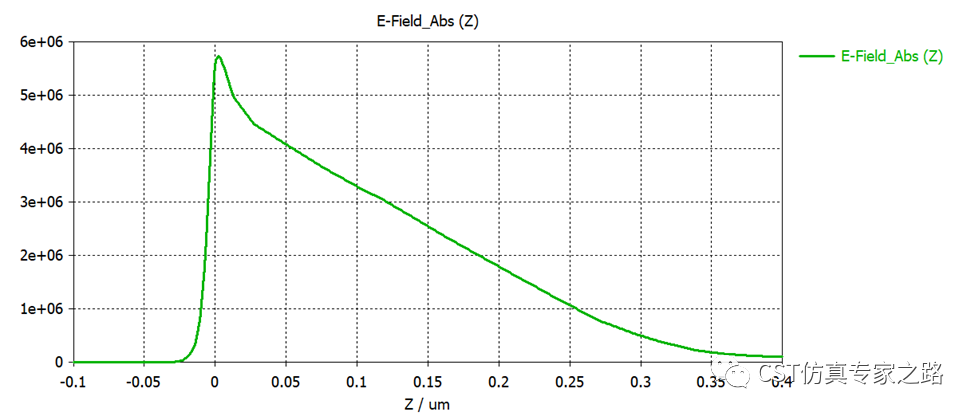

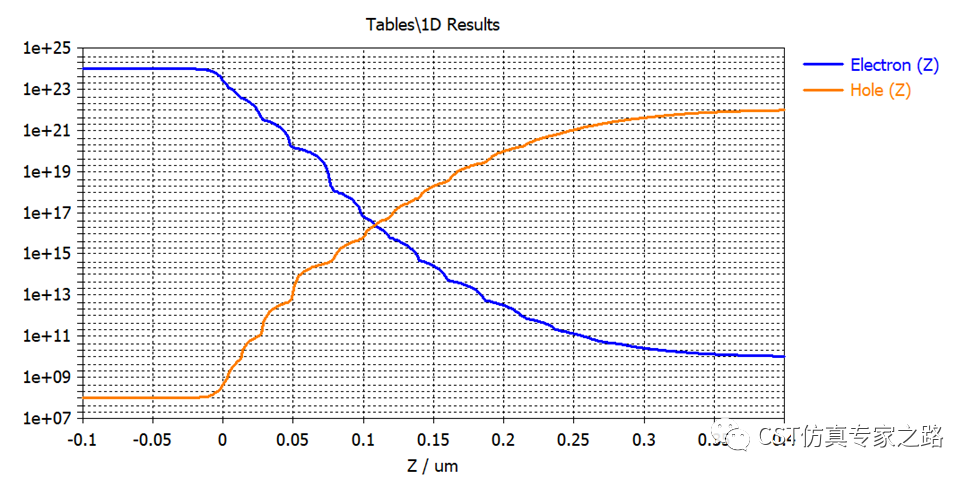
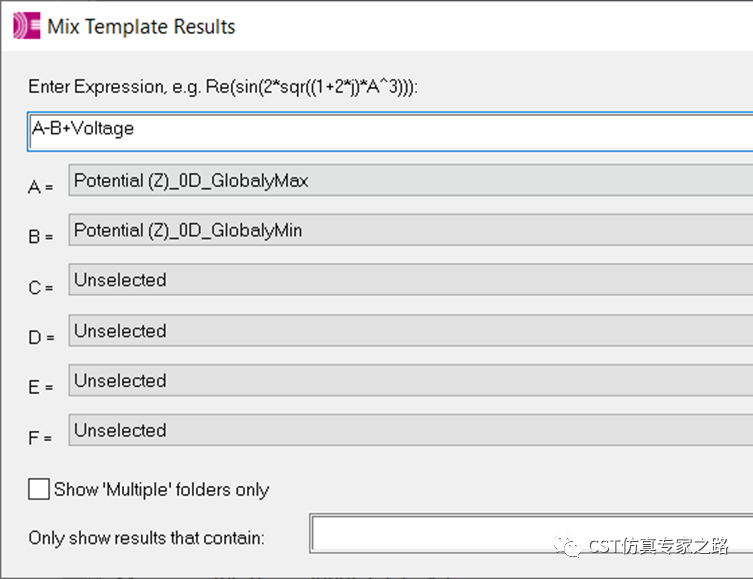
这里从这些曲线其实就能看出耗尽层的大概厚度了。还有三个后处理,其中两个是提取电势的最大值和最小值计算壁垒电势差;第三个是个mix template,用电势差加上外接电压voltage得到内置电位(built in potential)。
和我们之前手动计算的一致:
下面我们看看正向偏置电压,voltage=0.4V,重新仿真,对比电场和电势,符合理论预期:
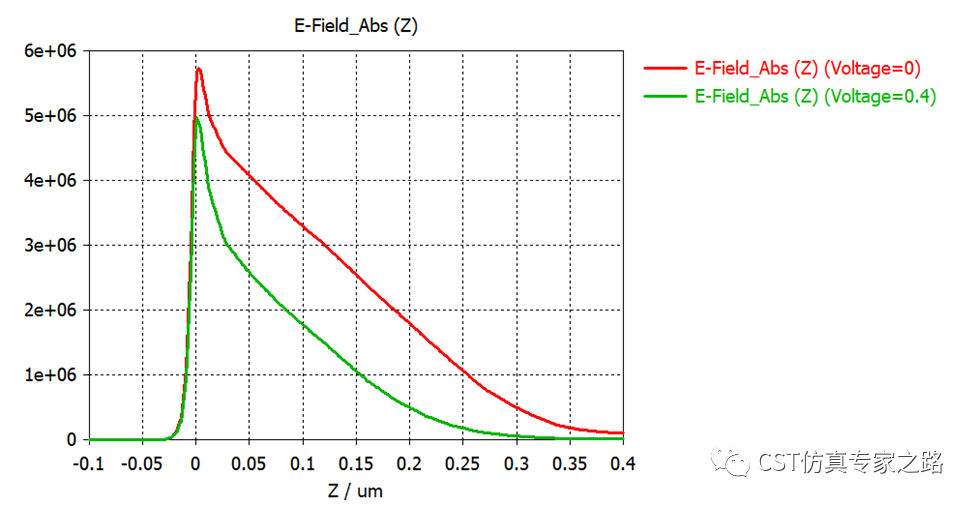
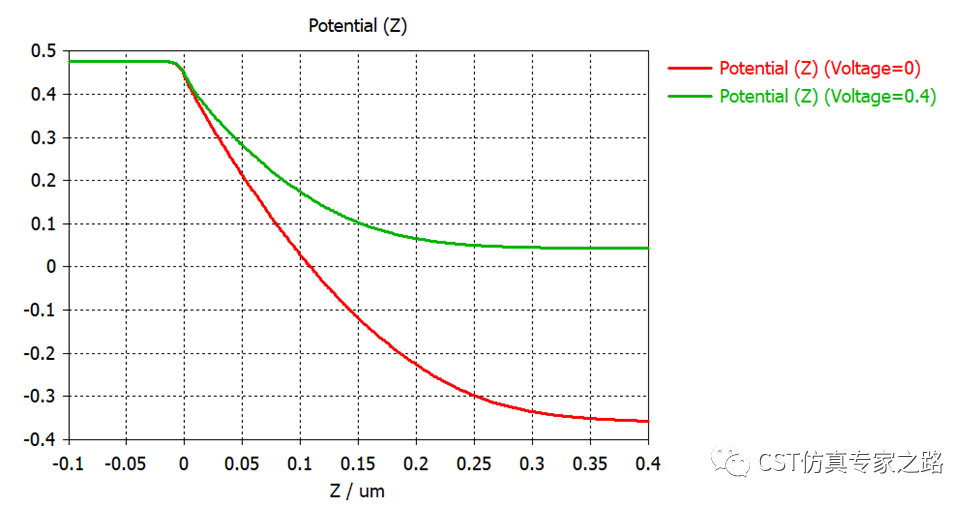
我们加个标尺大概量一下耗尽层约长0.25um:
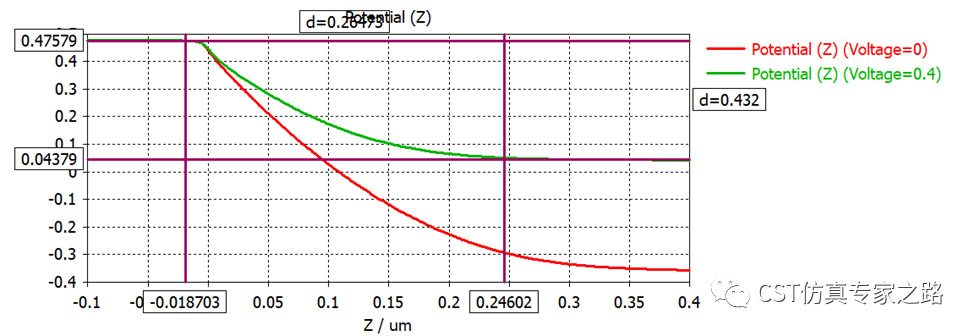
可用公式验证一下:
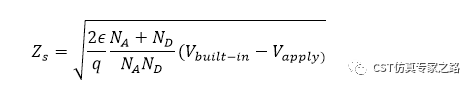
Width=sqrt(2*11.9*8.854e-12*(1e22+1e24)/1.602/1e^-19/1e22/1e24*0.43) =0.24um
有了偏置电压,空穴和电子的准费米能级也不同了:

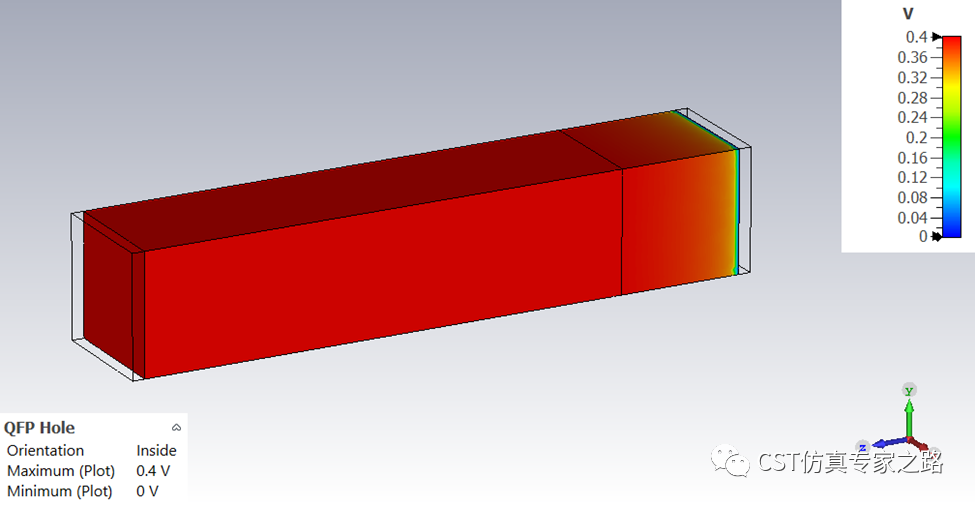
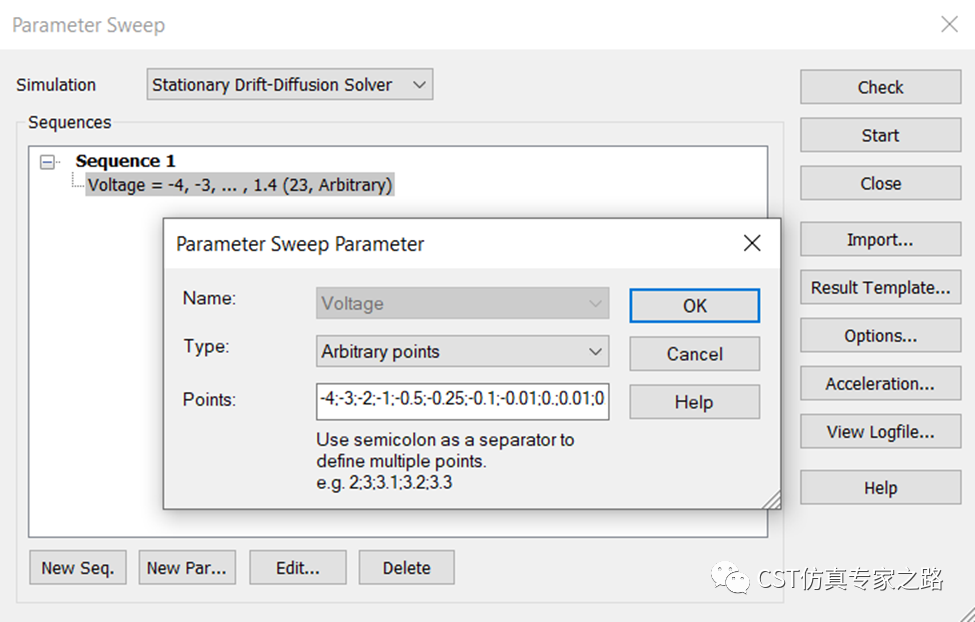
最后,我们扫参voltage,在0点附近多一些采样:
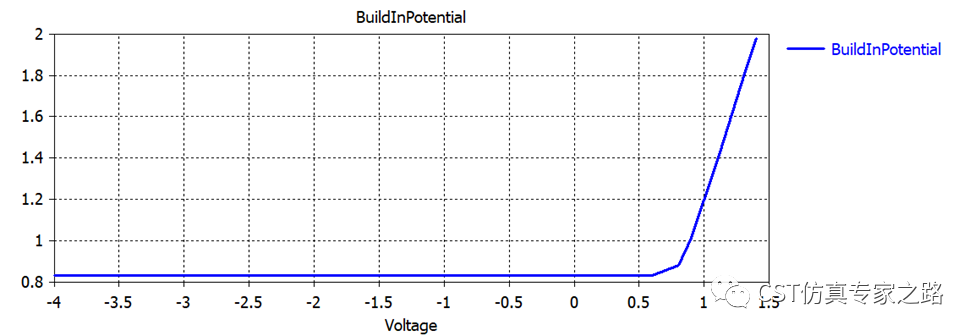
看内置电压,一直都是恒定0.83V,直到外界电压超过内置电压,大到把耗尽区完全压缩,PN结成了电压源。
查看I-V曲线,注意这里没有正负之分,方向可查看场图:
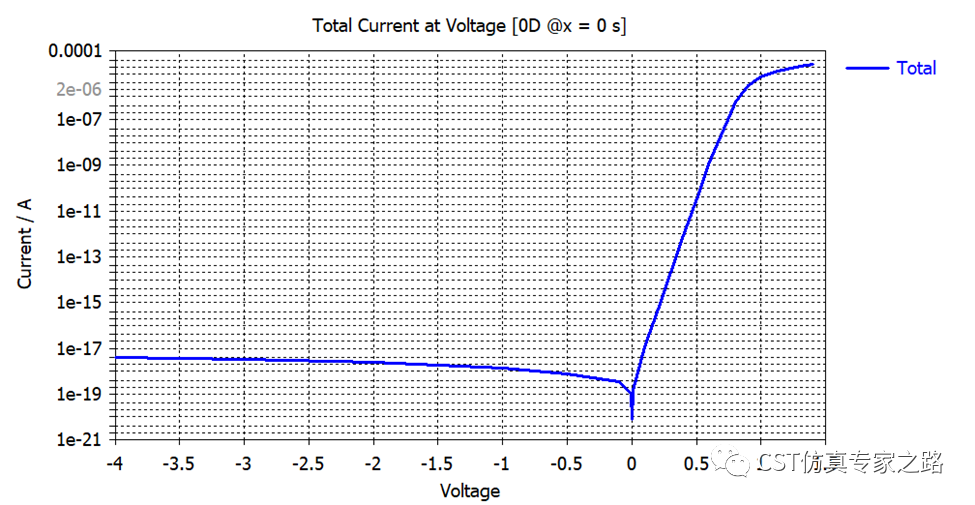
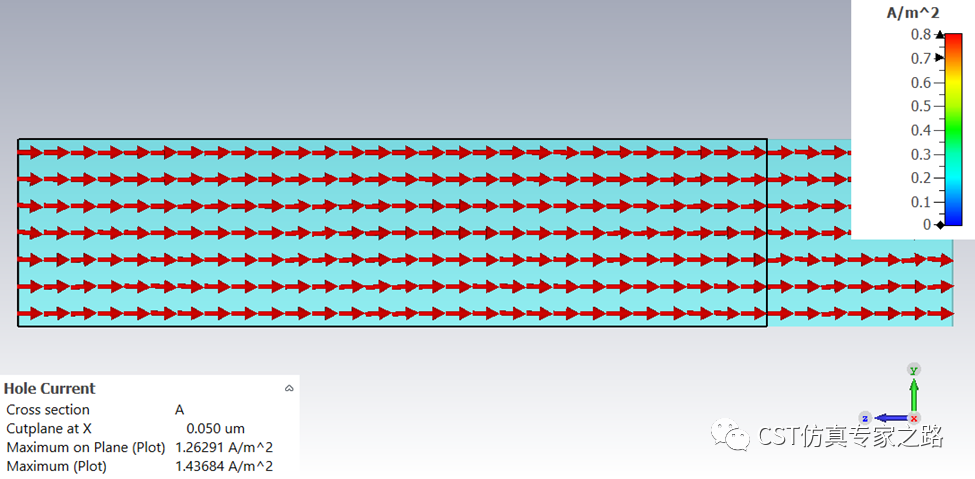
正向偏置的电流:
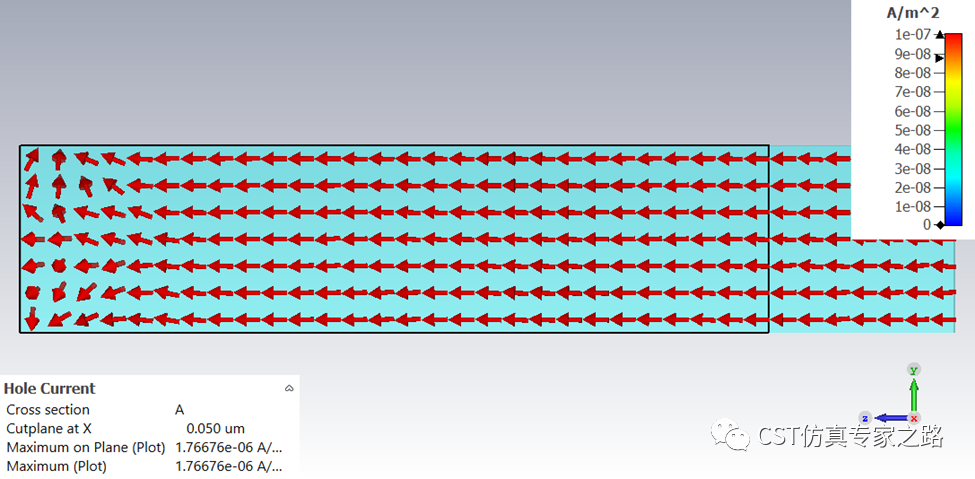
反向偏置的电流:
小结:
1. DD求解器是漂移扩散求解器,第一个D是drift漂移,计算施加电场下载流子定向运动;第二个D是diffusion扩散,计算载流子浓度变化效果。
2. CST可以用来分析半导体材料的导电特性,比如设计二极管。





