正方体RCS的CST仿真实例(2)- 双站RCS
来源:CST仿真专家之路
更新时间:2024-06-23
阅读:
本期还是以这个简单的自带案例为例,上一期已经看过它的时域设置和双站RCS的结果:
平面波一个方向入射:
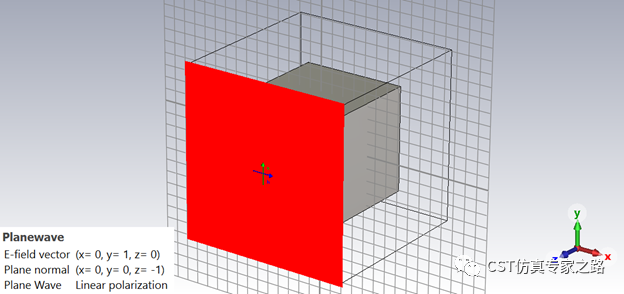
我们将后处理改成1D cartesian,截取phi=0平面的RCS值:
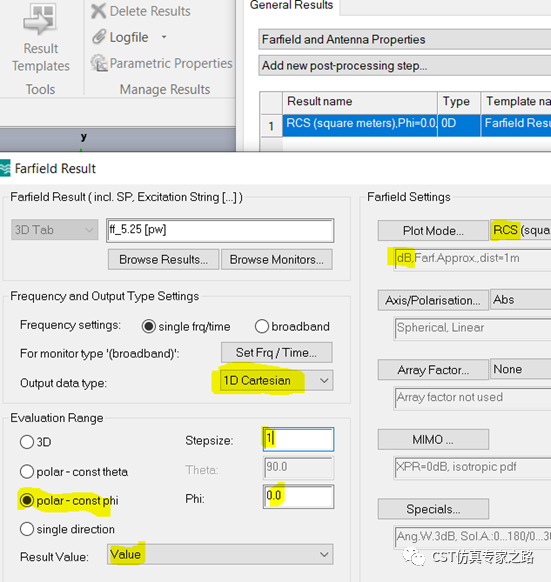
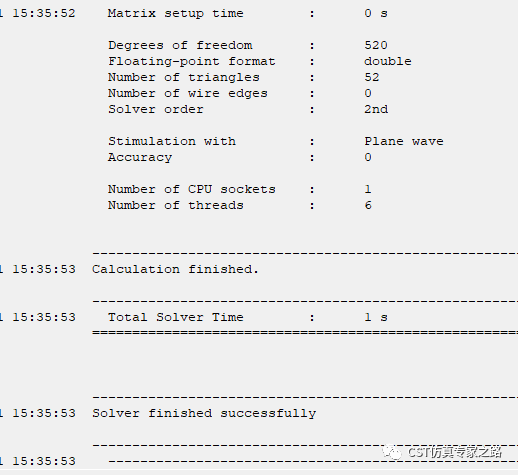
先看T-solver:
网格为六面体,有对称边界:
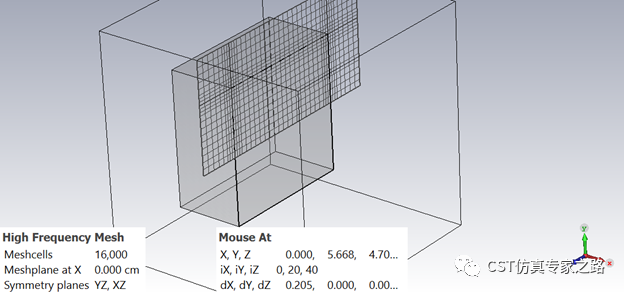
仿真结束后,将RCS曲线拷贝到新1D结果文件夹中:
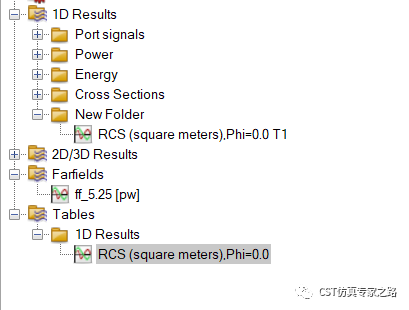
文件另存为,然后换去I-solver:
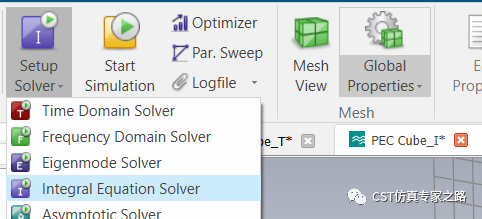
注意网格也要换去表面网格:
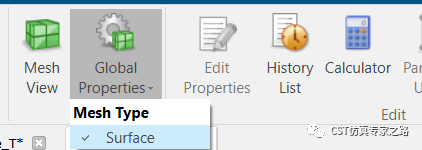
用默认精度先仿一次对比看看:
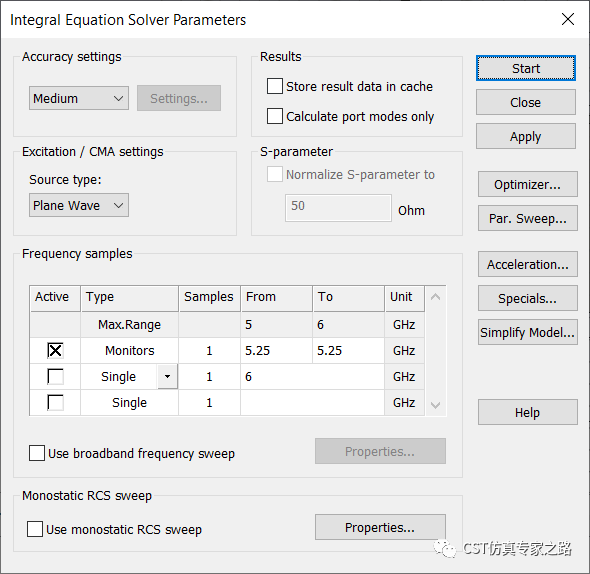
表面网格(背景无网格):

同样,仿真结束后,拷贝RCS曲线:

文件另存为,然后改去频域F-solver:

网格改成四面体:
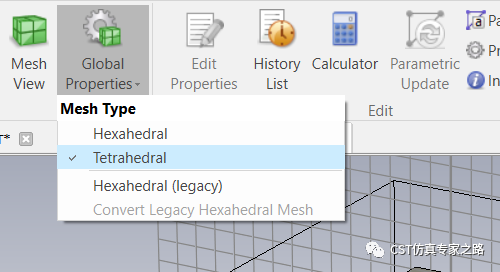
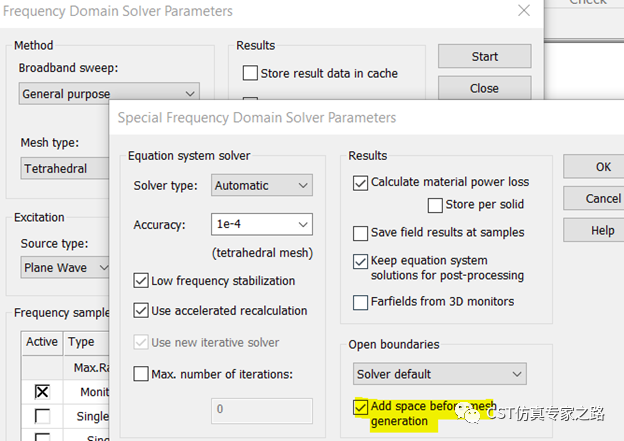
F 求解器中增加一些背景距离:
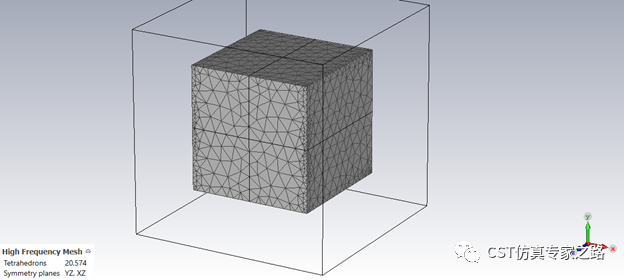
默认带8次的自适应网格加密,仿真后的网格:
三个结果一起看:

可见三个求解器的结果最大差别在0.5dB左右,总体一致性是不错的。
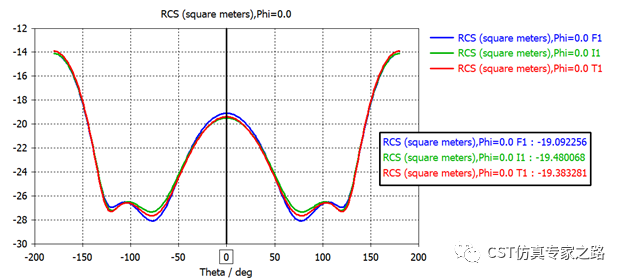
本案例计算RCS效率最高的是I-solver,只需要表面网格计算即可。下面我们看下提高精度对比,I-solver中设置:

对于T和F的精度提高,方法并不唯一,由于是全波计算,所以推荐的是加密网格,然后拓展一些边界距离和吸收,最后求解器的级数也可增加。三个求解器提高精度后,对比如下,可见误差已经在0.1dB以内。
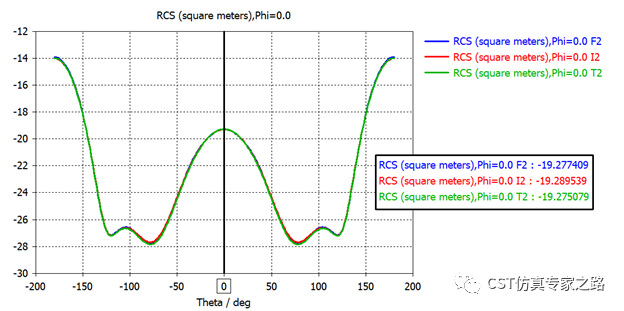
小结:
1)双站RCS就是平面波加远场。
2)电小尺寸的RCS计算可用T,F,I。I一般说适合电大尺寸,但本案例较简单,又是单频点,I效率也很高。
3)本案例I求解器(加精度之后)笔记本也只需要几秒钟: