电磁热耦合计算探讨三
上次提到了电磁热耦合的难点之材料的电磁特性。其实要非常准确的仿真电磁热问题还涉及到热力学的材料属性。尽量在OPERA内用公式法去描述(拟合)材料的特性会比较方便。实在复杂的就用函数结合table去实现。
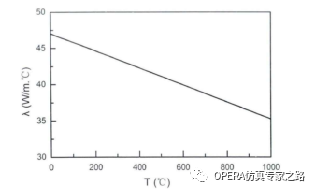
首先关于热导率,定义为单位温度梯度作用下物体内所产生的热流密度。像一般的低碳合金钢和铜等金属热导率几乎和温度成线性关系(如下图)。所以可以用直线带负斜率的公式(Y=kX+b)代表热导率随温度的变化。
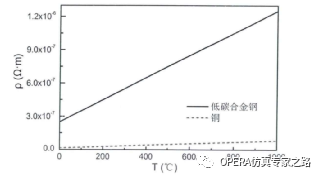
电阻率(电导率)和温度的关系也雷同:
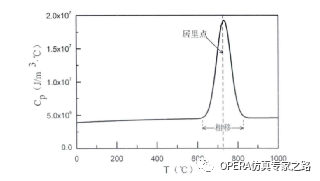
比热容就复杂了,比热容定义为单位质量物体升高或者下降1℃吸收放出的能量。低碳合金钢等金属比热容和温度是成非线性关系的。使用的描述公式还需要包含二阶相移(距离点附近由于产生顺磁现象引起的材料内部结构变化,相移过程中需要吸收大量热)。高度非线性。
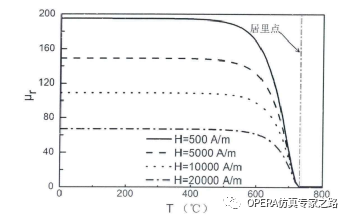
相对磁导率不止和温度T有关,还和激励的磁场强度H有关。可以看成Ur(T,H)函数,在OPERA内也可以直接定义。不同的H对应不同的T VS Ur曲线。当温度超过居里点时,相对磁导率就为1了。
另外温度变化也受散热条件的影响,有些感应加热器件为旋转器件,温度需要在短时间内升到居里点。那么这时候需要知道换热系数以及辐射散热系数。
这两个系数都需要参照环境温度。对流换热系数参照的是T的一次方关系。辐射系数是使用黑体辐射公式是T的四次方关系。在温度越高的时候,辐射散热占比会越来越高。
上一篇文有提到,电磁场和温度场的时间步长差距太大,所以计算方案是电磁场计算稳态场,温度场计算瞬态场。将电磁场的一个电周期内的发热功率计算出来,然后插值到温度场,计算瞬态温度场上升直到升温比如10度,这时候材料属性根据温度的上升也重新修正,然后继续插值过去计算温度场,可以加入停止条件为温度场不再上升停止,也可以不加就一直计算到总时间步到。大致逻辑图如下:
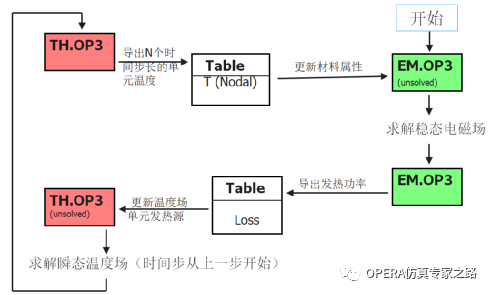
下回展示下在OPERA内实现的一个demo。
还是这个结论:电磁感应热的最大难点在于材料属性的获取,并非软件层面的操作。如果伙伴们哪天遇到谁只给你强调直接耦合、软件过程的,你懂的^_^ 个人认为电磁感应热在某些复杂情况下还是以趋势为主,绝对值的精度为辅。





