CST仿真实例：光子晶体微谐振腔分析和Q值提取

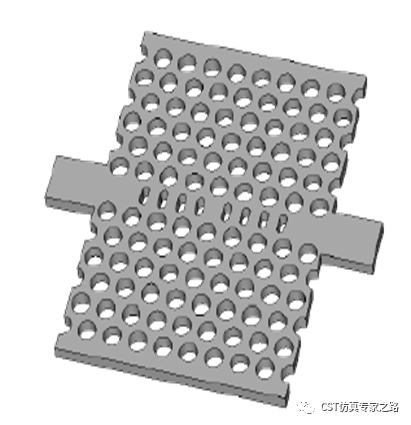
本期介绍基于文献[1]的一种二维光子晶体波导结构，利用路径上加微谐振腔来实现一些特殊的滤波功能。一般是要看谐振频率的变化和Q值变化，因为工艺误差或任何造成结构不规则的因素对这样细小的结构谐振来说影响非常大。下图为文献中提到的硅薄膜结构，中间路径上的8个椭圆柱体便是微谐振腔，4个一排算是布拉格反射器。

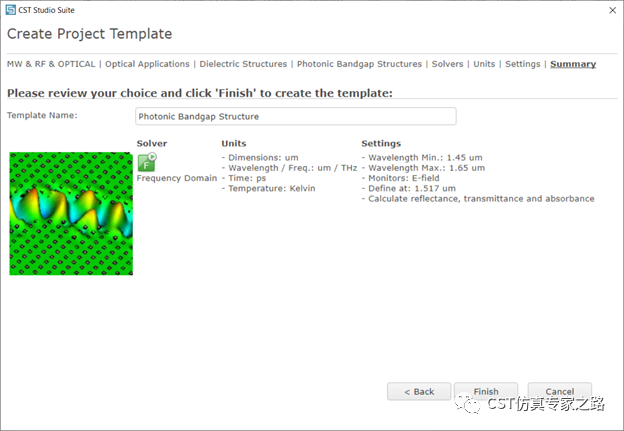
Step 1. 用光学应用模板

工作频率属于红外线，这里用F频域求解，因为要研究谐振腔。

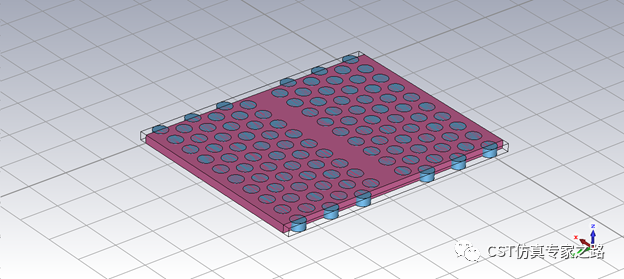
Step 2. 建模

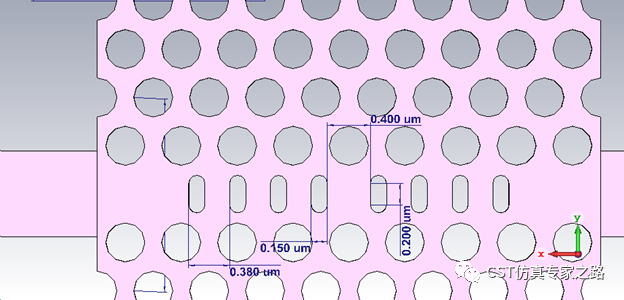
画法有很多种，这里我们先画空气柱，半径182nm，高205nm，周期520nm，用60度正弦算位移就行:520*sind(60)。

然后删去周围不用的圆柱，在画个方块作为硅薄膜，材料Silicon(opticalIR)，然后insert布尔运算。

两边加上宽800nm的传输线各一段。

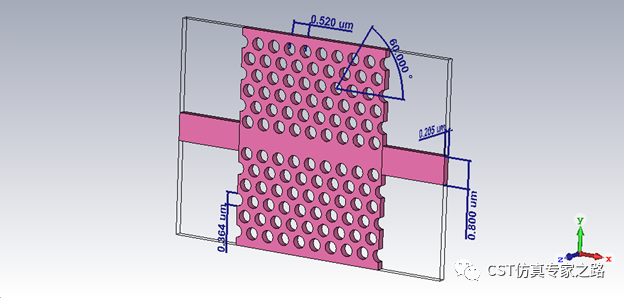
Step 3. 仿真

边界用open(add space)，为了加快仿真速度，XZ面电对称，XY面磁对称。这里强调一下，CST的PML边界精度二十年前就可以达到极低，是很高级很成熟的技术，不是所有的PML边界都能叫“完美吸收边界”的哦。

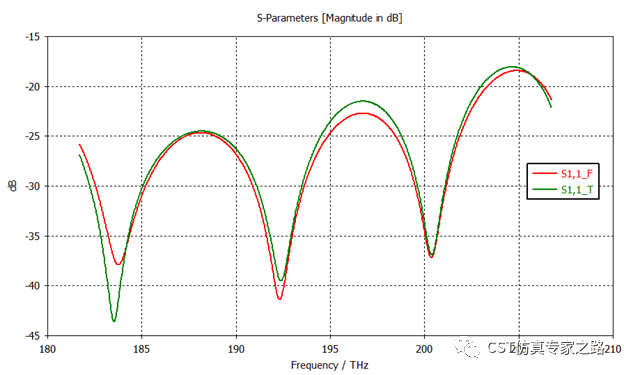
接下来就可以仿真了。其实T和F都可以，因为还没加微谐振腔。要想二者结果匹配的好，提高精度，加密网格，材料统一，尤其是非均匀的波导的端口模式和色散，都是关键。这里跳过设置细节，直接上结果，可以看到两个算法不同网格都能在THz拿到非常一致的结果。（当然想要再精确也可以，只要有时间继续等喽；谁再不相信CST时域谐振点算不准，出来挨打）

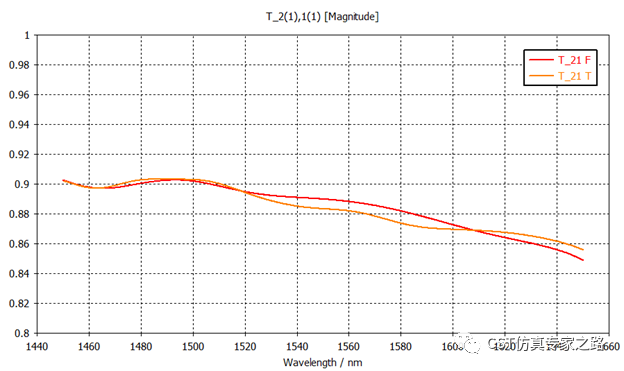
S21当然也一样好，这里直接看传输率，转换公式见之前的光传输线案例。

场监视器在1517nm，属于通带：

Step 4. 加微谐振腔

接下来就可以挖几个胶囊形的结构，可以画中间方块加上两边两个圆柱体，也可以画大方块然后把四个边做个blend切圆滑。位置就对称中心吧，其实x轴方向上移动位置是会影响谐振频率的。

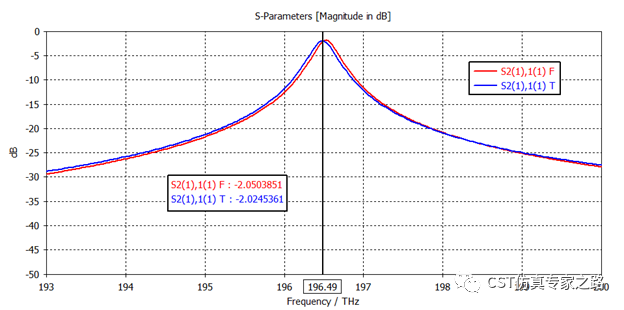
加上谐振腔之后就必须推荐F求解器了，因为T求解器会慢很多，能量收敛慢。但不是不能用T-solver啊，等的起没问题啊，这里我就任性一下，两个都用，为了展示一下结果对比。可见大部分频段都被反射，只有大概197 THz部分可以通过，所以是滤波效果。这个峰值是研究重点。

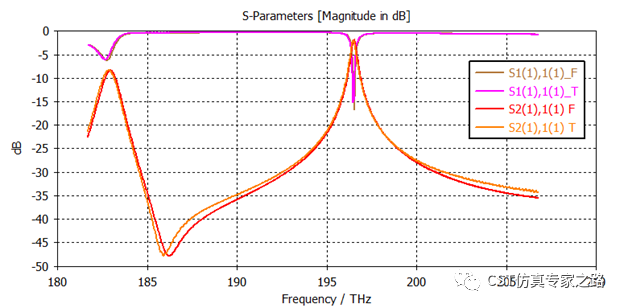
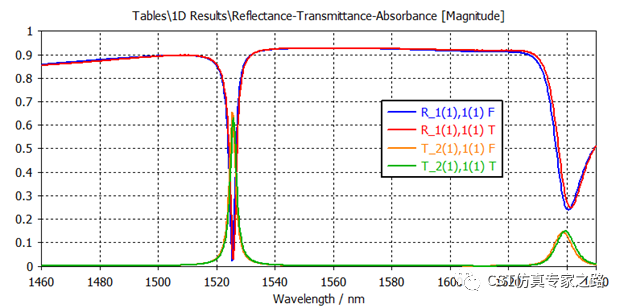
场监视器在1517nm，属于禁带：

Step 5. Q值运算

两个方法，从能量衰减一半计算，或者3dB频段来算，不管哪个方法，都需要先用x at Global y-Maximum后处理提取S21的峰值频率，我们命名为fn（fn不在下图）。

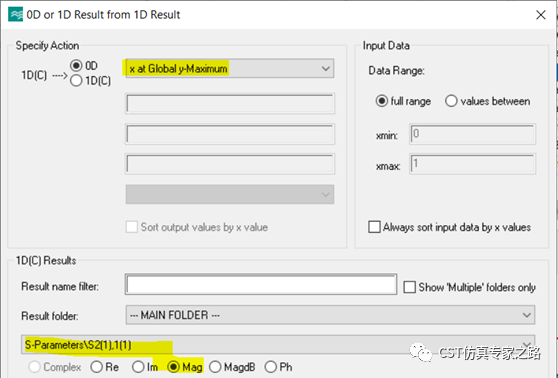
能量法：

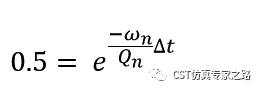
这个只能是时域结果用，因为需要能量衰减曲线，峰值频率fn乘以2pi就是，然后需要算出从能量曲线衰减一半所用时间t，最后Q就有了。这里用-20dB和-23dB对应的时间差算t。

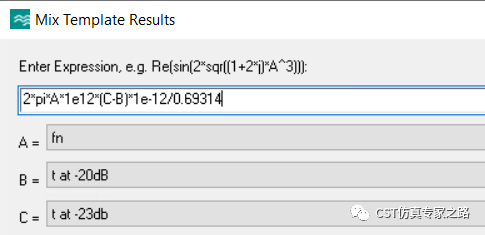
这里时域算出Q为587。

频段法：

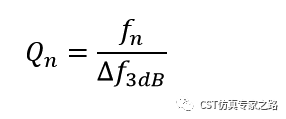
这个就容易些，时域频域都可以，有了S21，用3dB频段就可以：

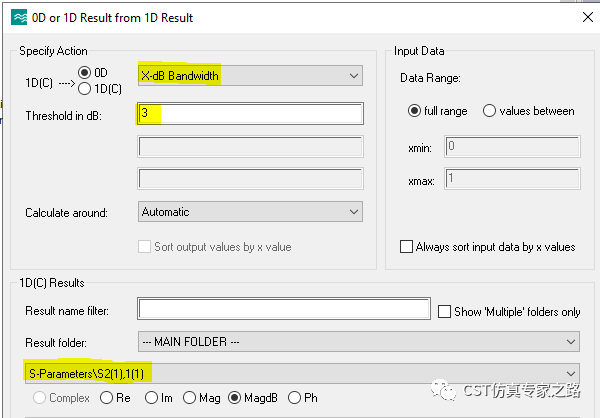
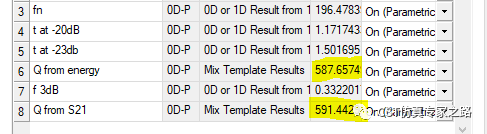
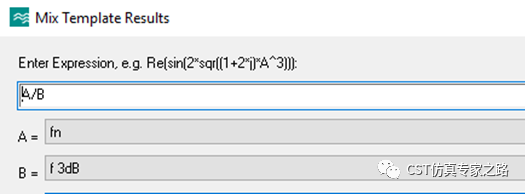
时域这里Q值算出来是591。

频域的话同样办法算出来是608。

其实误差就在于S21曲线准不准喽，所以仔细看S21，这一点点差别能造成Q值10-20的误差。

[1]：M"arki,I., Salt, M., & Herzig, H. P. (2006). Tuning the resonance of aphotonic crystal microcavity with an AFM probe. Optics Express, 14(7), 2969.doi:10.1364/oe.14.002969