超材料SRR-wire单元和等效材料参数提取CST仿真实例
这一期我们看超材料中经典的SRR-wire单元,背部加上导线的缺口环形共振器,作为左手材料(LHM)或双负材料(DNG)的基础,演示等效材料提取方法。
Step1. 单元的建模与仿真
这里基板尺寸5x5x1mm,材料介电常数epsilon为3.84,tangD=0.008,频率范围5-12GHz; 金属为PEC薄片,厚度0.017mm。边长、间距、开口、宽度都可自由定义分析,会影响震荡频率和带宽。

Z方向为磁场极化,PMC边界,磁场穿过缺口环形中心,产生磁震荡;Y方向为电场极化,PEC边界,电场顺着导线方向,产生电激励。
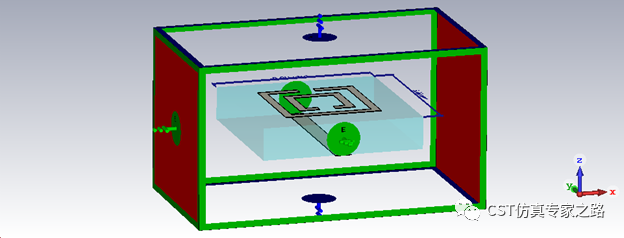
X方向对称,PEC边界,各增加一定背景距离,定义两端波导端口并将参考面移至SSR,这样可以保证相位从SSR边缘开始算,并且端口接触材料为均匀背景空间。Z方向上背景距离加2mm, 所以等效的单元为中间部分5x5x5mm的正方体,等效厚度为X方向上的5mm。

这里我们只激励端口一,模式一,提高精度后,F和T不同算法算出来的S参数结果比较是非常准确的。可以预测震荡频率应该在9GHz附近。
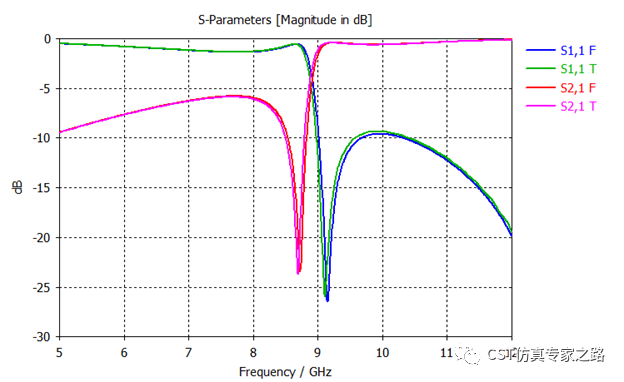
Step 2. 提取等效材料参数
运行后处理S-Parameter ->Extract Material Properties from S-Parameters。该后处理基于文献[1],是一种S参数反演法。这里S参数我们用之前两个求解器的结果之一,有效厚度便是X方向上的5mm。m是文献中的折射率n实部的”branch index”,是针对复自然对数或反三角函数的无穷个数解的严谨定义。这里设默认0即可,适用于单元等效厚度远小于波长。
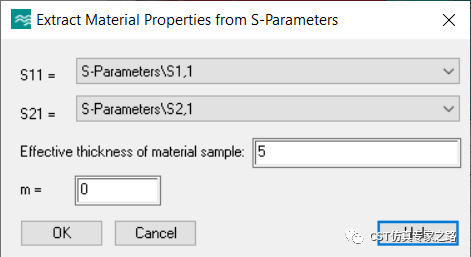
运行之后,新的结果文件夹生成,相关材料参数都有。z是相对阻抗,n是等效折射率,ExpTerm是文献中的指数表达式。
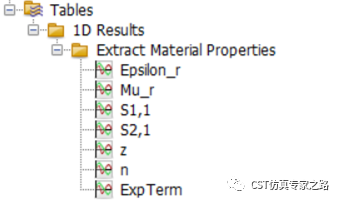
等效的介电常数Epsilon_r和磁导率Mu_r如下图,可以看到在8.8-9.2GHz左右便为左手材料双负区域。在震荡频率附近或有S参数噪音区域,该文献[1]的方法也不能完全保证虚部在所有频率大于零的无源性。比如我们看到提取的Epsilon在8.8GHz有一点点波动(反共振),这种非匀质性问题很多文献都有讨论过,比如[2]。
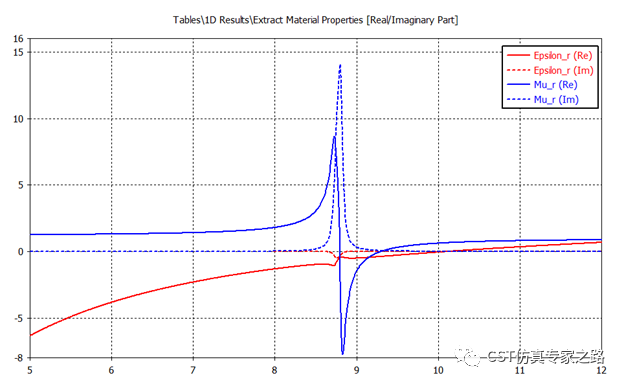
或直接查看折射率n,也可以清晰看到负折射率区域。
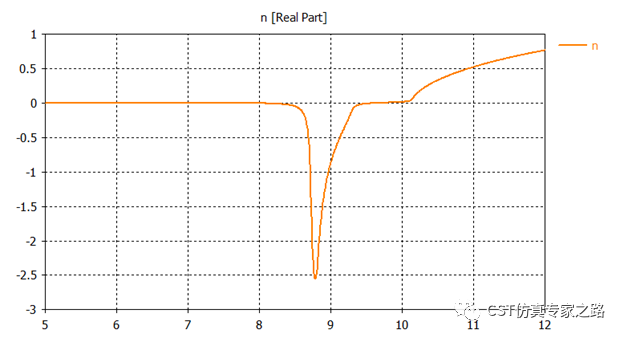
然后这些等效的材料数据可以ASCII格式导出,用于等效单元。
Step 3. 等效单元验证
新建一个CST模型,5x5x5mm的正方体,两边端口同样推参考面到结构。
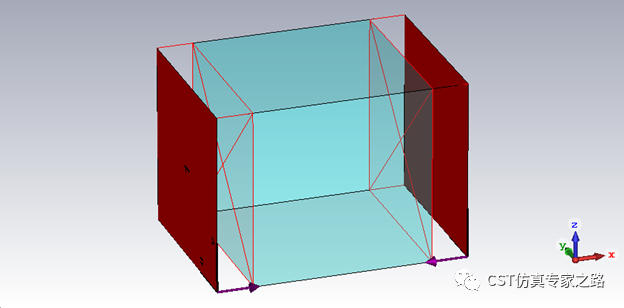
正方体的材料为新定义的材料名bulk,类别为normal,dispersion用导入上一步导出的材料参数。
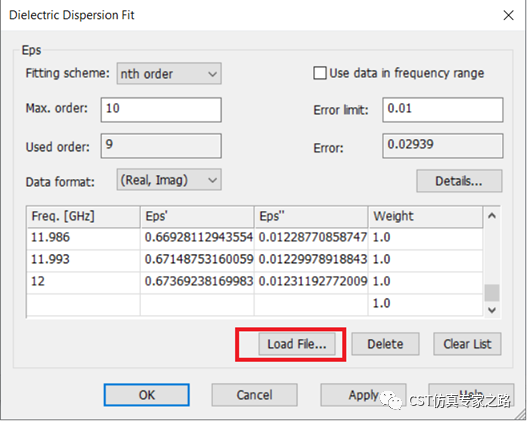
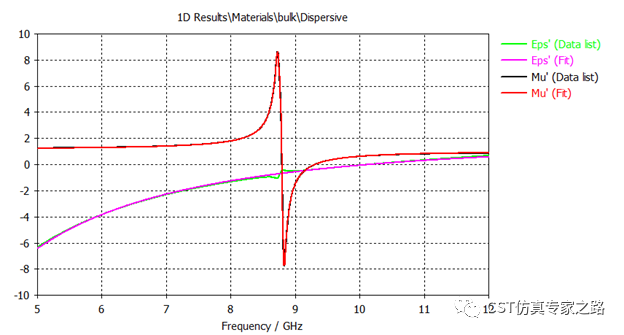
虽然是提取的参数直接导入,但求解之前材料自动拟合还需要一个过程,本案例用高阶的拟合,同时忽略8.8GHz的小波动,下图为求解器拟合(Fit)的效果查看,然后可以开始仿真。
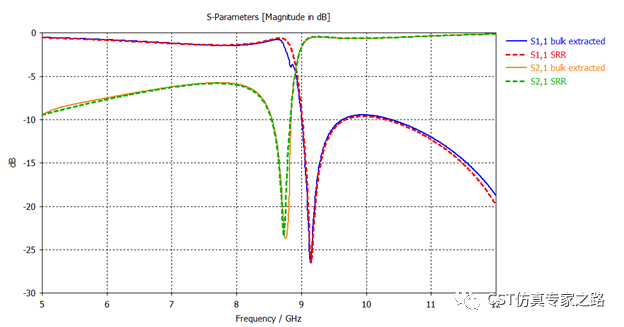
仿真结果基本相同,这里SRR是取之前T和F两个验证过的结果之一。这里表示该正方体加上bulk材料能够等效准确地代替之前的SRR结构。
为了了解结构的传播特性,可以加3D场监视器。下面的磁场传播动图便可看出在8.85GHz,等效盒子内的传播是反方向的。注意这里激励信号从-X方向输入(从左到右传播),若背景距离长一些则视觉效果更好。

通过以上三个步骤,我们就得到了所谓左手材料的等效结构和等效材料参数。
补充内容1.
接下来补充另一个等效材料的建模,利用冷等离子材料的Drude模型,结合磁共振常用的Lorentz模型。也就是说,我们可以选择不用上述提取再导入的方法,这次换成Drude-Lorentz模型直接生成材料曲线。材料定义界面,输入以下参数便可以大致拟合出我们得到的两条材料曲线。当然,这些参数需要一定数学优化工作和经验值范围加快优化效率。
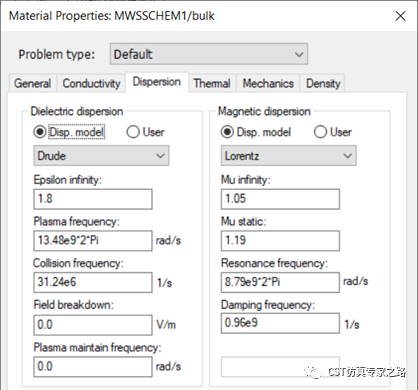
Drude的参数相对容易(公式参考help),可根据定义来调试,无穷大处的epsilon为常数,用来调整个色散曲线的高度。等离子频率越高,epsilon越低,可以调色散曲线的斜度,最后碰撞频率量级较小,影响不大。Lorentz的参数复杂一点(公式参考help),无穷大处的Mu一般就是1多一点,静磁场Mu比无穷大处的Mu大一点,差值决定总体Mu的水平。Resonance frequency 就输入我们观察到的8.8GHz的振荡频率,Damping frequency 用来调整震荡的幅值。
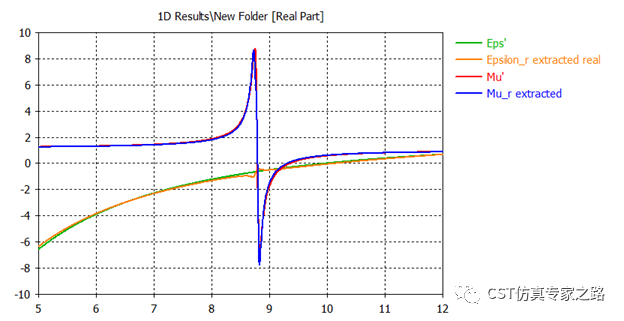
这里们比较Drude-Lorentz生成的材料曲线和由S参数反演(后处理模板)提取曲线比较,二者差别也不大。
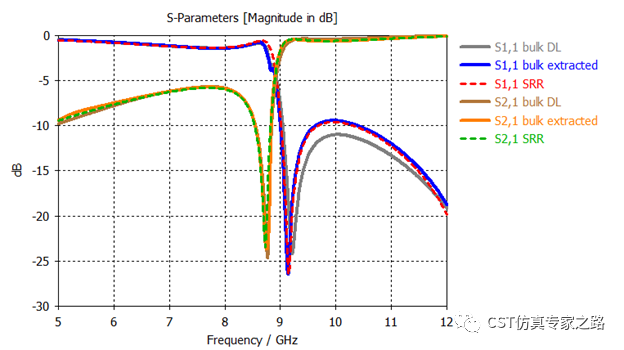
最后,对应的S参数结果三种方法大致相同。当然,要想更精确,材料的实部虚部都要拟合的更好。
有了等效材料,就可以根据需要替代SRR-wire单元,比如这个喇叭天线:
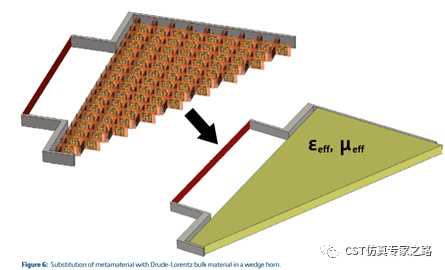
左图为右手材料频率,右图为左手材料频率:
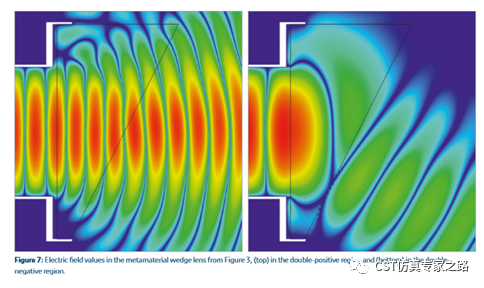
图片来源和更多超材料资料请看:https://discover.3ds.com/behavior-of-metamaterials
最后划重点:
1)单元分析震荡频率是超材料分析的第一步。
2)S参数的反演法获取等效材料曲线由CST后处理完成,比较简单。
3)Drude-Lorentz模型获取等效材料曲线需要手动拟合,比较复杂。
4)两种办法拟合的都不错,但都不算完美,有更好的提取或拟合文献欢迎讨论。
5)总体来说利用SRR-wire震荡的超材料还是有体积大,带宽窄的缺点,以后我们有机会再介绍其他不用震荡的左手材料结构。
[1] Chen, X.,Grzegorczyk, T. M., Wu, B.-I., Pacheco, J., & Kong, J. A. (2004). Robustmethod to retrieve the constitutive effective parameters of metamaterials.Physical Review E, 70(1). doi: 10.1103/physreve.70.016608
[2] David Smith et al.; Electromagnetic parameter retrievalfrom inhomogeneous metamaterials: Phys. Rev. E 71, 036617 (2005).





