如何验证“平面波+探针”的频域结果

我们以金属球加平面波为例，平面波从Z+方向入射，频率0-5GHz。

球的半径为1cm。其实什么结构不重要，重要的是定义两个探针，一个近场（边界内），一个远场（边界外），然后研究探针的探测结果。这里时域求解器，不检查能量收敛，让平面波足够时间传播到两个探针。

仿真结束后，应该可以得到这些结果：

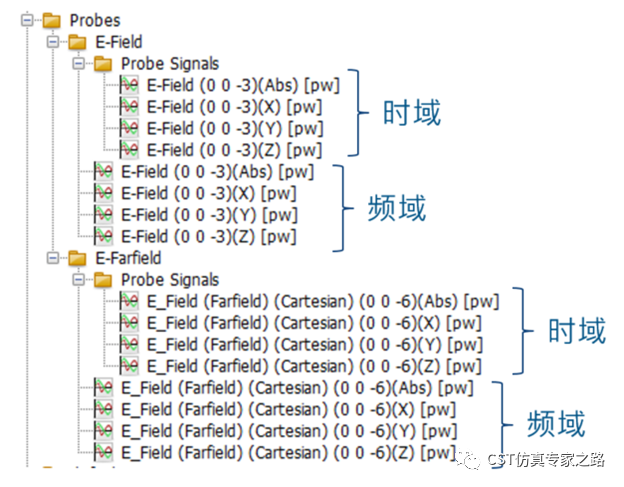
由于这里平面波电场极化方向为X，探针得到的信号主要也是X方向，我们就看有（X）的结果。Y和Z方向结果忽略。

情况1 ：FIT+默认的高斯激励信号

这种情况下，频域探针结果会针对默认信号进行归一。

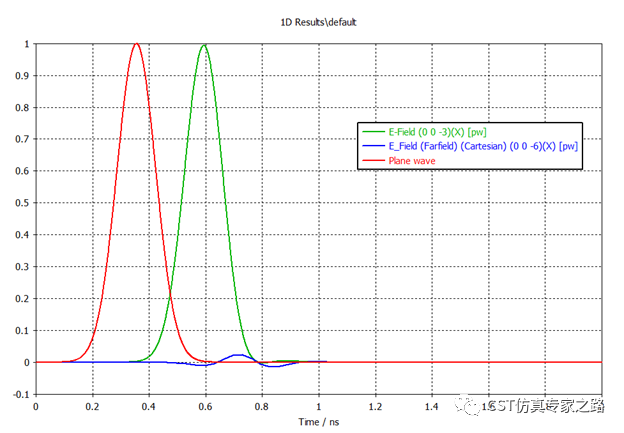
首先先把时域结果加上平面波信号放一起，三个结果有个传播上的时间差，这个很好理解。值得注意的是，远场探针的信号很弱，因为平面波基本被Z-方向的边界条件吸收，远场也只是结构散射得到的结果，毕竟这里仿的不是天线。换句话说，平面波的仿真中，远场探针基本无意义，我们还是拿来一起展示。

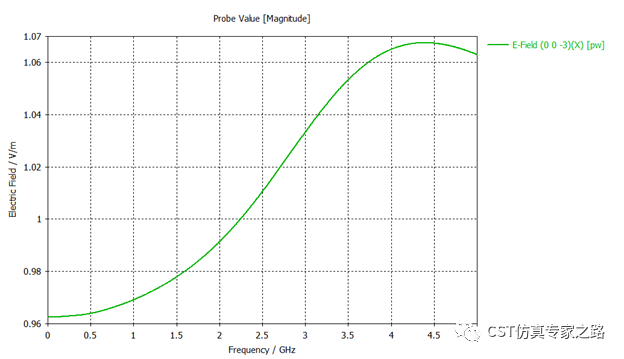
好，回到频域，刚才说这种情况下，频域探针结果会针对默认信号进行归一，先看近场探针频域结果，可见幅度为1上下，这就是针对激励信号归一的结果。

然后我们用后处理，把对应的时域信号做个傅里叶变换成频域：

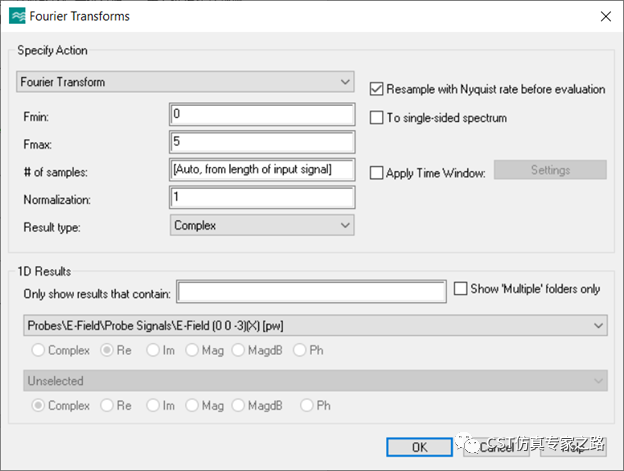
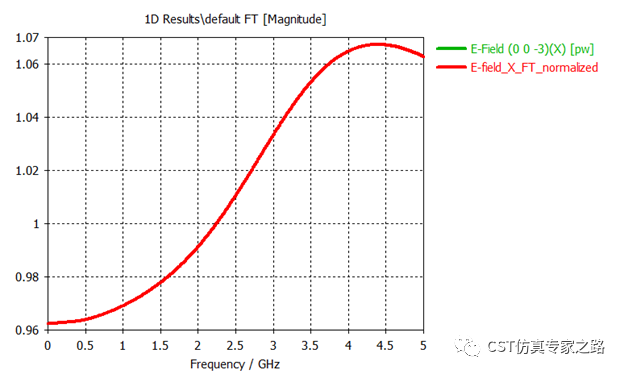
得到以下频域结果。怎么样？差别很大吧?不光纵坐标量级变了，上升下降的趋势也不同，这就是没有对激励信号归一化。

那么如何将其调整成一样的呢？我们可以手动归一化：我们把这个傅里叶变换的结果称为A，再计算一下激励信号的傅里叶变换结果，称为B，然后用A/B：

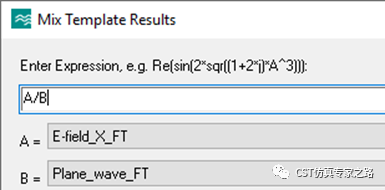
得到的频域振幅就一样了：

当然还没看相位：

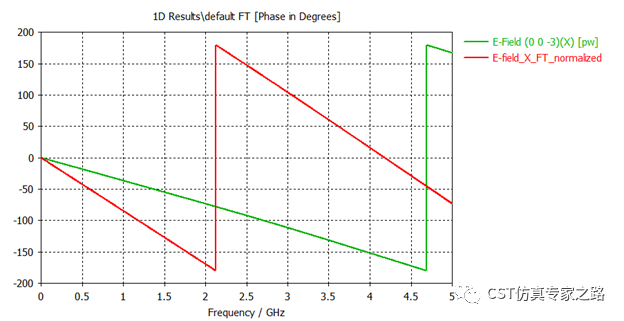
诶？振幅一样，相位却还不一样。这是因为，探针的频域和时域，处理平面波的相位参考位置不同。

如帮助文档所解释，平面波的相位参考是坐标中心零点，这是指频域，而时域的相位参考则是平面波发射过来的位置，也就是Z+边界。

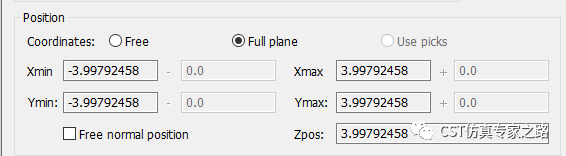
那么既然边界用的open（add space），怎么确定Z+边界的位置呢？这里可以用个小技巧，点击波导端口，就能自动检测边界位置，所以这里平面波位置是Z=3.9979。

然后就是归一化时要考虑这段3.9979cm的传播相位了，我们知道复数的相位是可以用自然指数函数exp(j)调整，所以我们改进刚才的归一公式，加上相位调整：

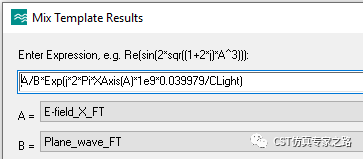
这里的XAxis(A)是0-5GHz,乘1e9就是Hz，0.039979除光速就是传播时间差，然后相位就一样了：

近场探针结果验证完成，其实远场探针也可以用同样方法验证，这里我们省略步骤，直接看振幅和相位：

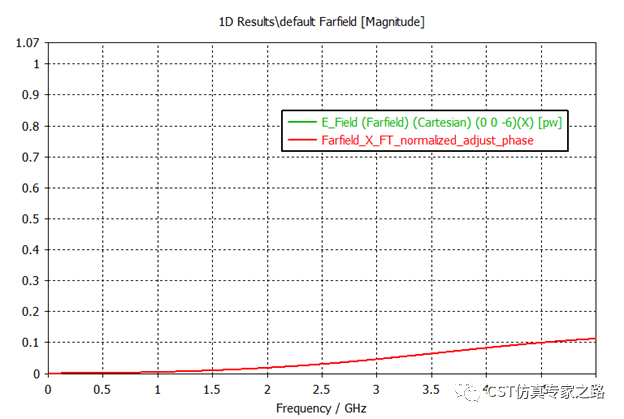
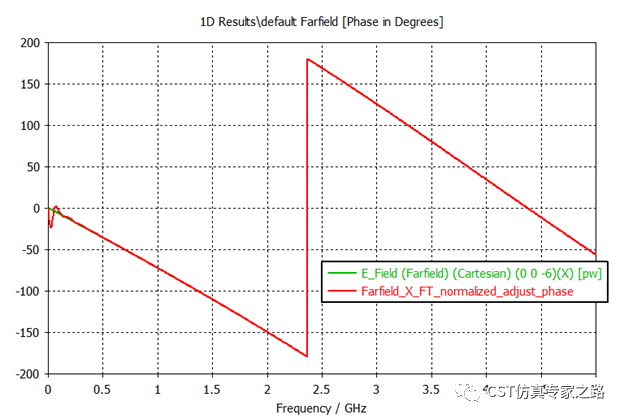
可见远场验证结果也一致，除了低频振幅的计算有点误差，这是因为在这种低频，Z=-6cm的远场位置不算远，应属近场，所以不够准。

情况2：FIT+自定义激励信号

这种情况就有可能探针结果不归一，为什么说有可能呢，因为归不归一取决于时域的这个设置，也可以看到标注说默认信号一直都有归一化。

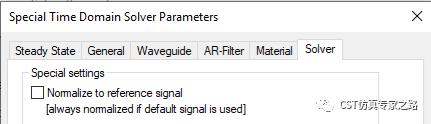
所以这里我们尝试不归一，就是不选，为了看验证探针的公式有什么变化。信号我们从默认的0-5GHz高斯脉冲，改成3-4GHz的脉冲，同样先看时域信号，时间差一样，因为探针位置不变，远场探针接收信号依旧很弱。

然后验证近场探针频域结果，还是对时域做傅里叶变换，为了和探针的频域相比较。频率范围改成3-4GHz：

可以看到，傅里叶变换直接就可以拿到同样的振幅，不需要手动归一化：

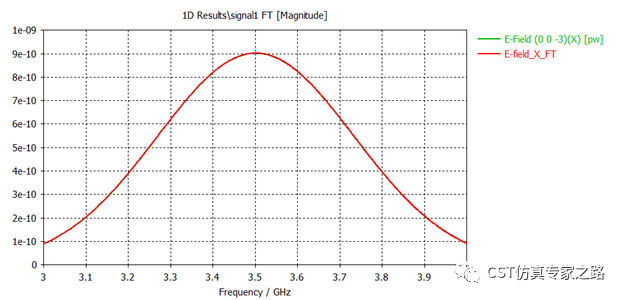
但是，相位依然不同。所以，我们说的时域求解器对信号归一化，通常只是归一化振幅。

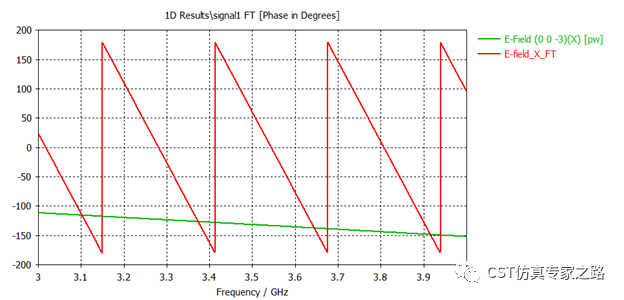
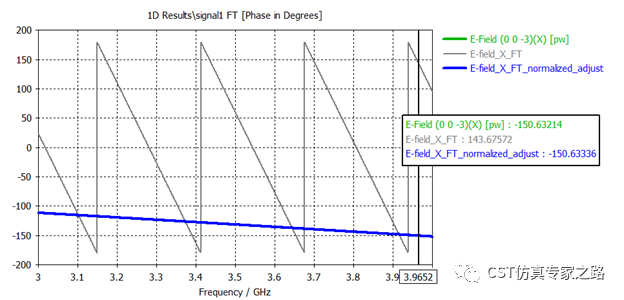
所以，这里相位要想达到一致，还是需要手动归一化，并且加上相位调整。这里因为振幅不需归一化，所有相位归一时就要补回振幅，我们加上个Mag(B)。

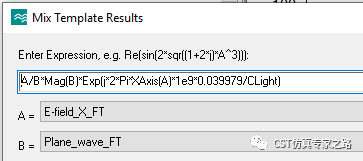
然后相位就一样了：

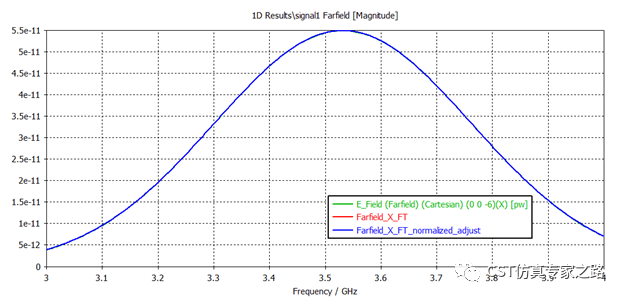
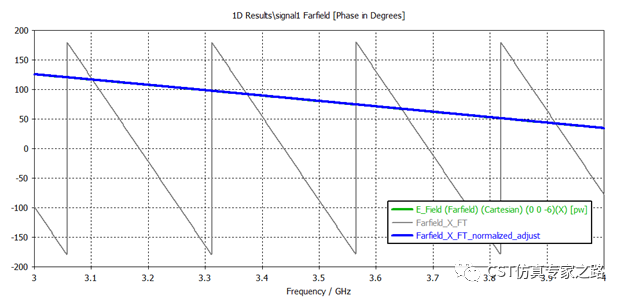
同样方法，远场振幅和相位也可以对的上：

情况3: TLM+默认Impulse信号

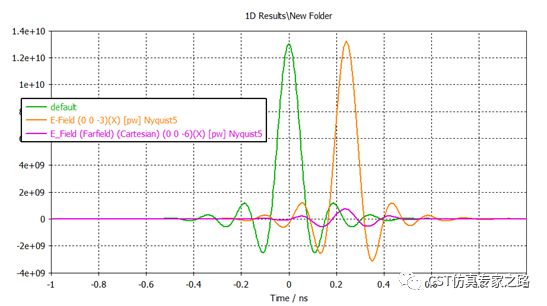
TLM的默认信号是Impulse，不是高斯，所以三个时域信号（0-5GHz）是这样的：

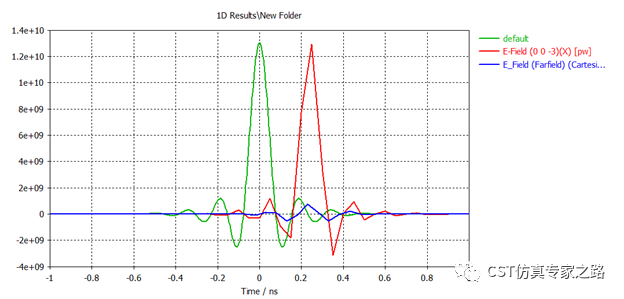
可见探针的采样不够多，需要在求解器设置更高的采样，比如Nyquist*5或Nyquist*10，这样时域信号会更平滑，当然仿真时间也越长。

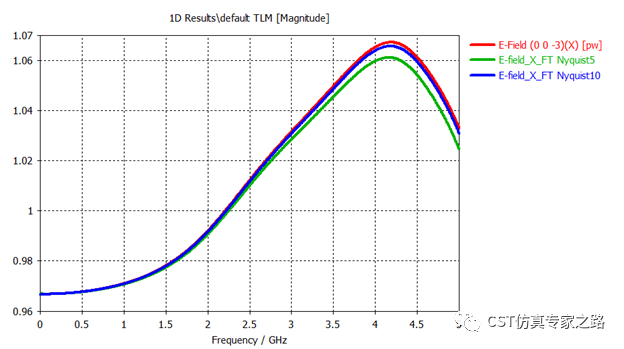
而且频域结果也随着采样增加而一致，这里可以看出频域结果是自动振幅都归一化好的，因为激励信号是没有归一化的。

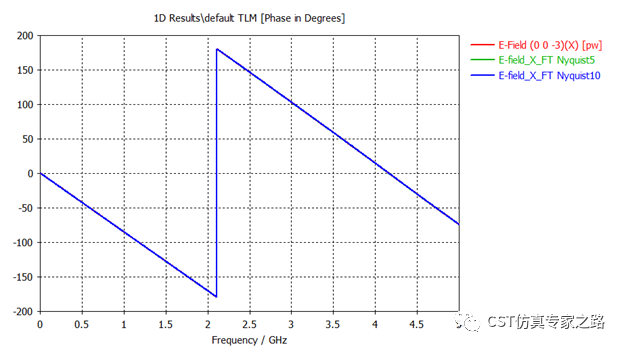
而相位无需归一和调整参考点，就可以验证。

当然，并不是所有的TLM激励信号都不需要归一或调整参考点，这里我们就不讨论其他信号了，方法都一样。

最后总结：

1）近场探针和远场探针本质还是有区别的，中间隔着吸收边界所以效果截然不同。建议远场一定要远，不然计算有误差。根据实际距离好好定义，别像本文举的例子，明明两个探针距离结构都很近，非要一个近场一个远场。

2）傅里叶变换可以验证时域频域结果，振幅要注意归一化，相位要注意归一化和参考点。

3）目前各求解器归一化情况比较复杂，参考点也不同也不好理解，这是因为要照顾更多应用场景，比如RCS扫描或EMP；所以只要用户知道自己在干什么就行，今后版本策略会改也说不定。