超材料光子晶体CST仿真 - 60度周期布里渊区与布洛赫定理
之前写过二维光子晶体的案例:超材料光子晶体和禁带分析实例,其周期为正方形
这期我们还以二维光子晶体为例,看一下六边形周期结构的色散图仿真,以及多重模式下利用布洛赫定理进行模式挑选。
第一部分:建模和仿真设置
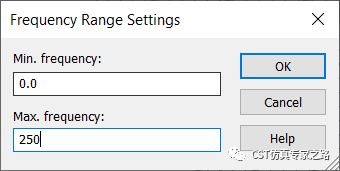
首先推荐使用色散图模板,频率范围设0-250THz。
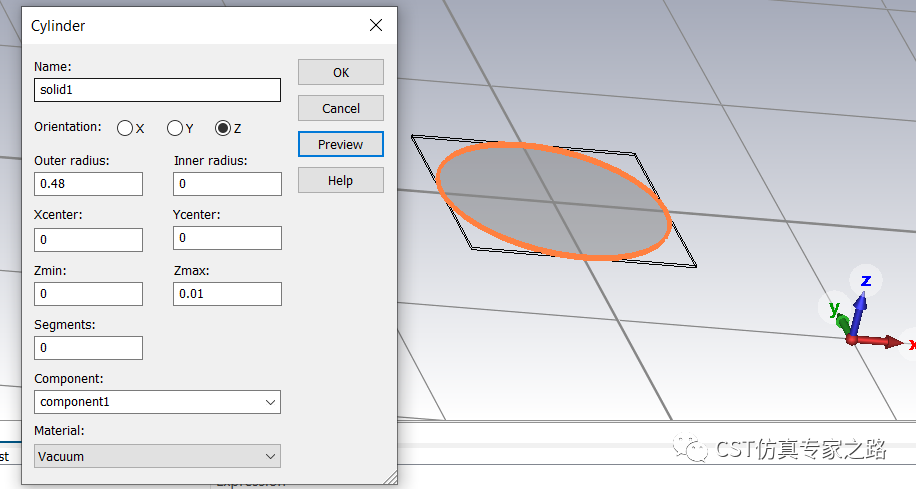
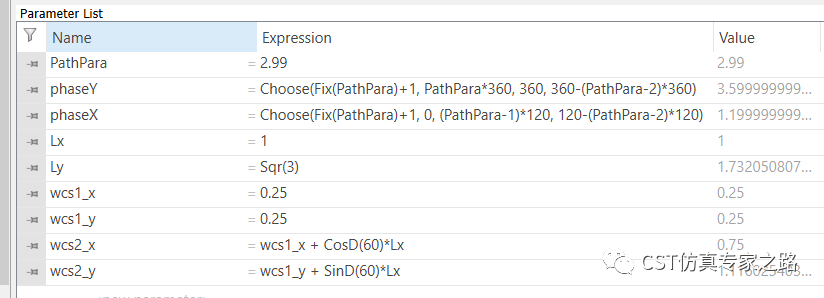
定义周期结构尺寸参数:

建模:
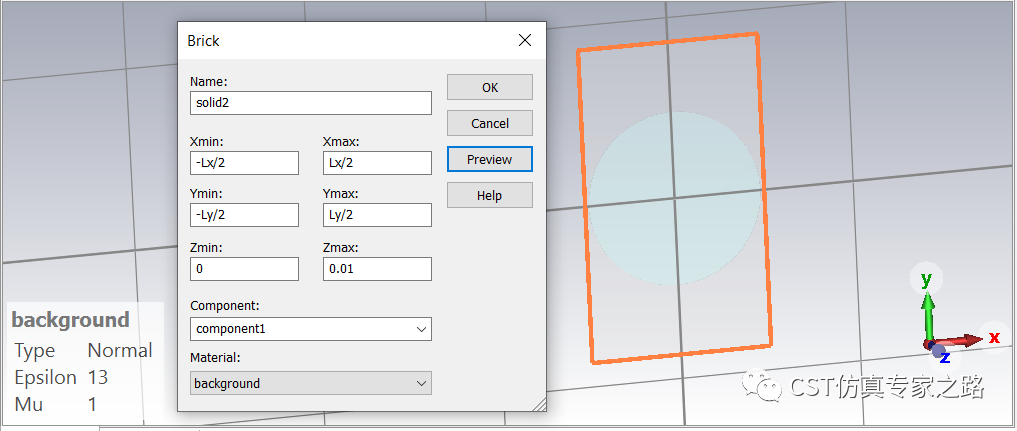
再画个方型区域作为单元晶胞,用圆柱Trim。
复制周期单元,剪切,只保留方形区域内单元:
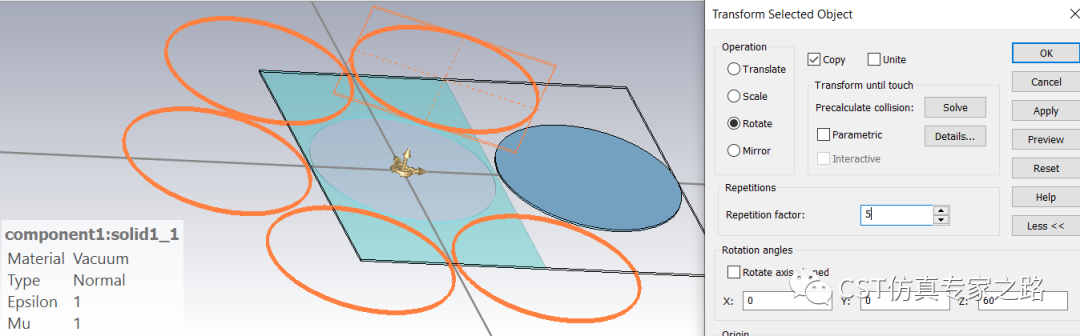
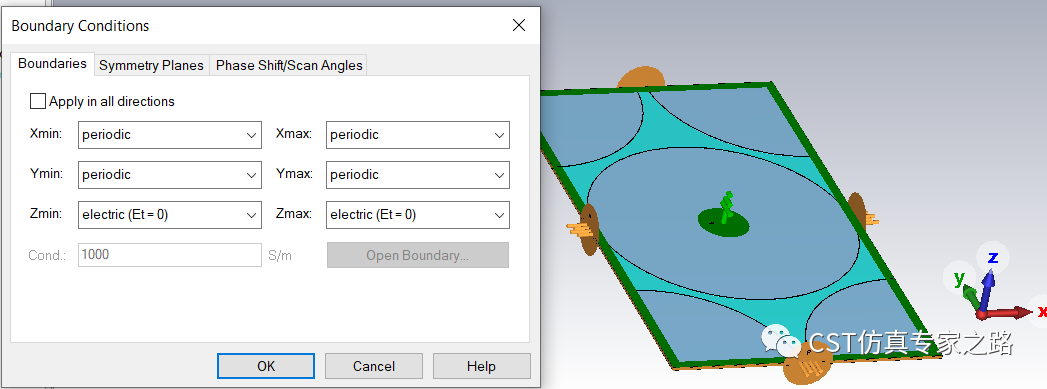
求解器设置:
提高求解器精度和速度:
手动加密网格:
先添加后处理方便后处理:

六边形不可约布里渊区:
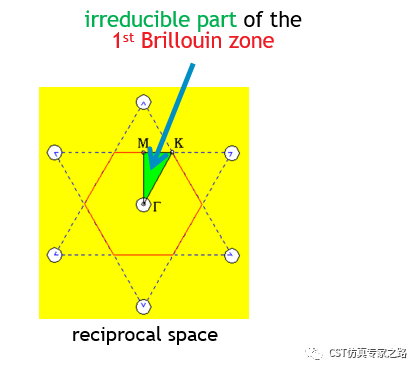
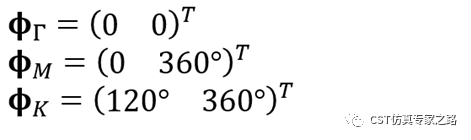
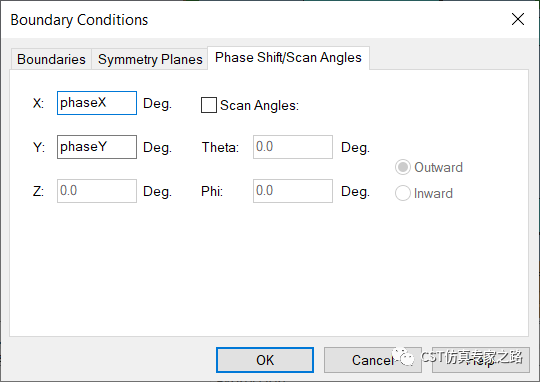
Γ→M: phaseX=0; phaseY=0~360
M→K: phaseX=0~120;phaseY=360
K→Γ: phaseX = 120~0;phaseY=360~0
所以修改phaseX和phaseY的定义式:

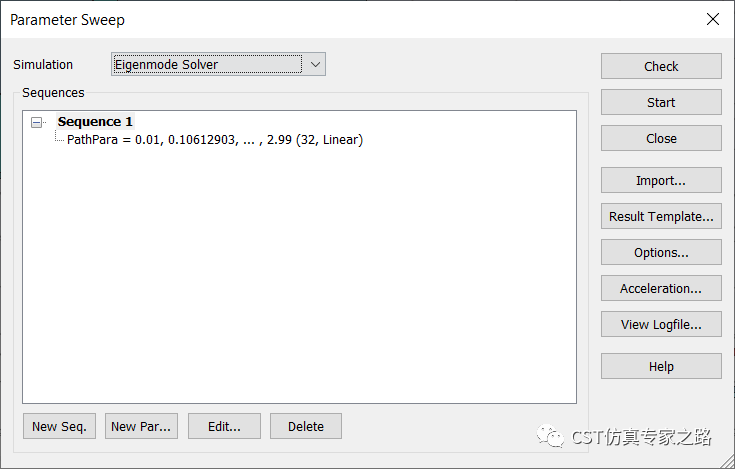
参数扫描开始:
第二部分:布洛赫定理验证
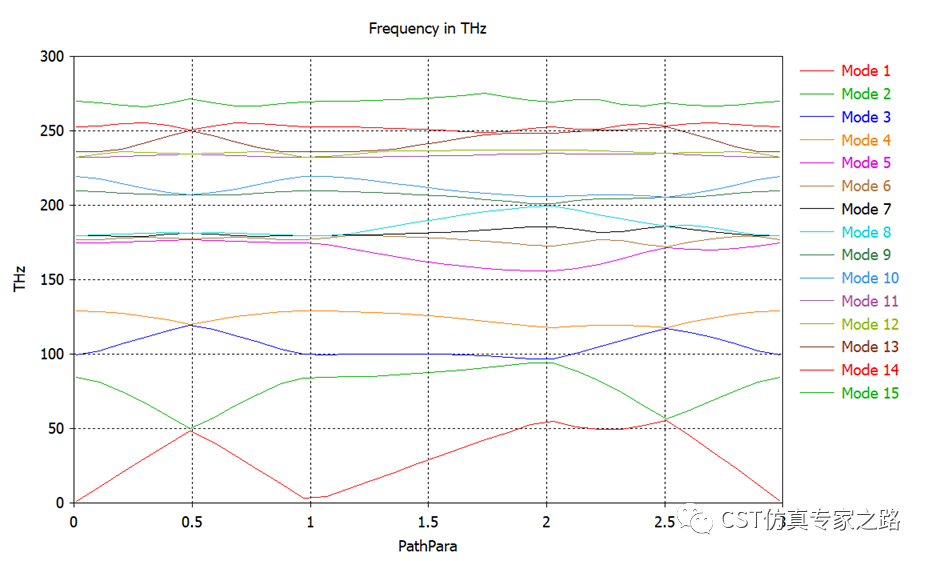
由于相位计算k的结果是非唯一解,所以该结果中会有出现多个Mode表示一个TM模的混乱情况。我们将通过后处理,手动验证真正的TM模是哪些。
根据布洛赫定理,本征模需要满足下式:
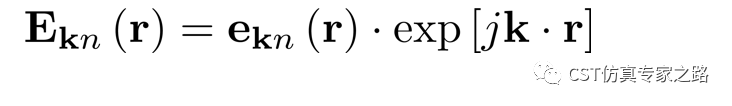
其中e是晶格周期函数,E是本征模,所以,反用公式可得周期函数表达式:
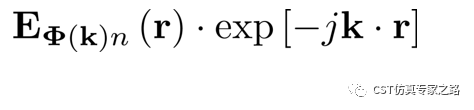
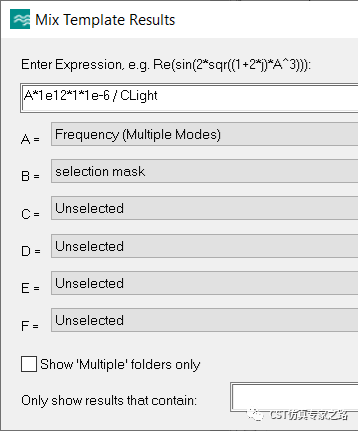
具体方法就是,在三维结构中,我们定义两个圆曲线,相对位置为晶格矢量,然后分别计算曲线上的Z电场(TM模)或Z磁场(TE模),然后与相位因子exp相乘,作为满足晶格周期函数的本征模电场,再和之前计算出的15个Mode相比较,选出符合布洛赫定理的Mode。
由于场数据存在采样误差或其他误差,我们不能期望提取的函数表达式完全准确(也没必要),所以可用统计学中的变异系数(Coefficient of variation),比如设个阙值0.05,小过这个值我们就认为两组数据相同。相同的区域就保留Mode曲线,不相同就是不符合布洛赫定理的无效Mode曲线。
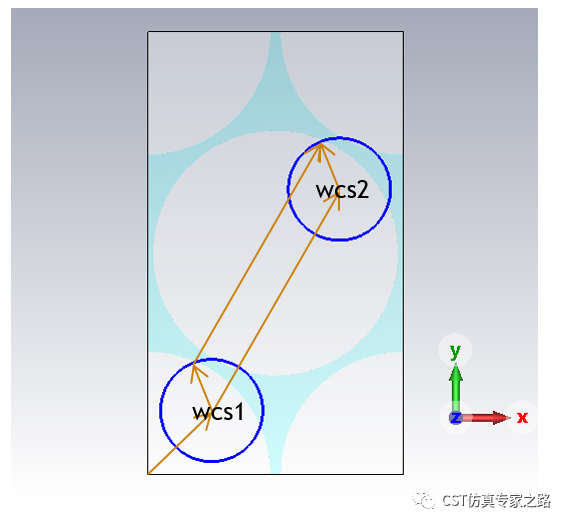
WCS放到角上,厚度中心,以该点为参考,定义两个WCS的坐标,方便我们计算晶格矢量。
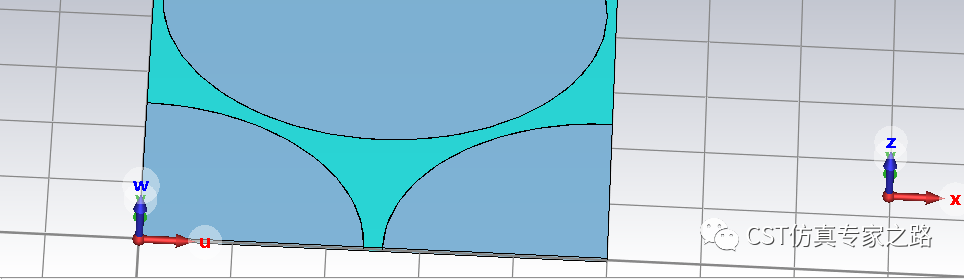
将WCS移到第一个点,储存为wcs1,画个圆半径0.2,所以该圆是以u轴开始的逆时针方向。
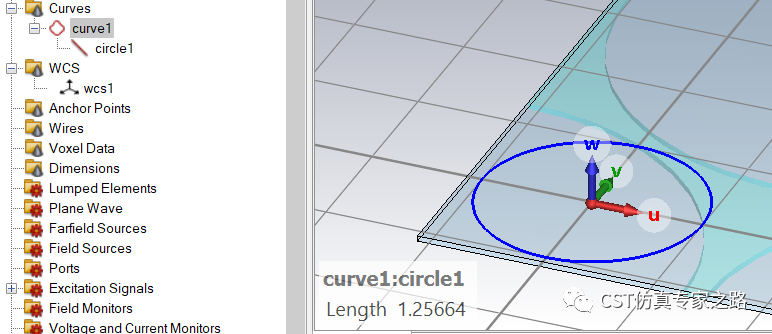
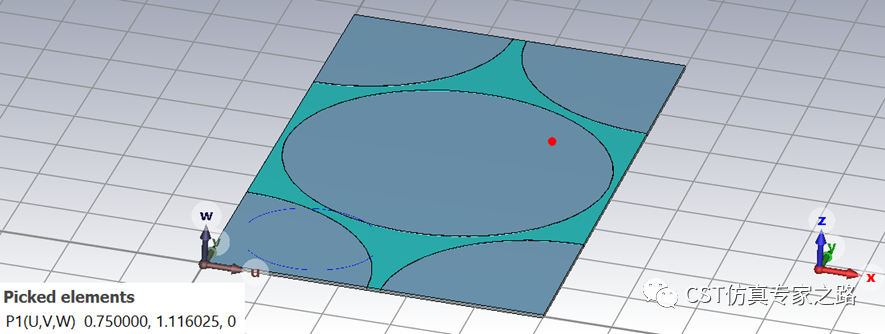
再将WCS对齐到第二个点(可用pick point from coordinates,需还原WCS到参考点), 储存为wcs2,画个圆,注意要分开成第二组曲线。
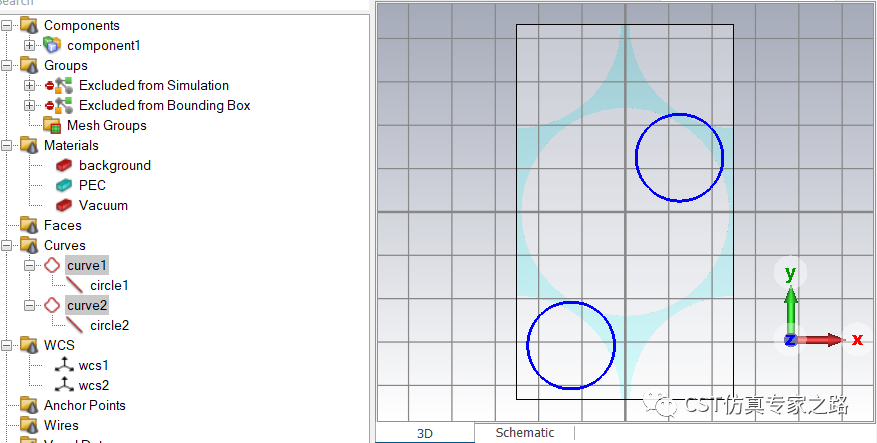
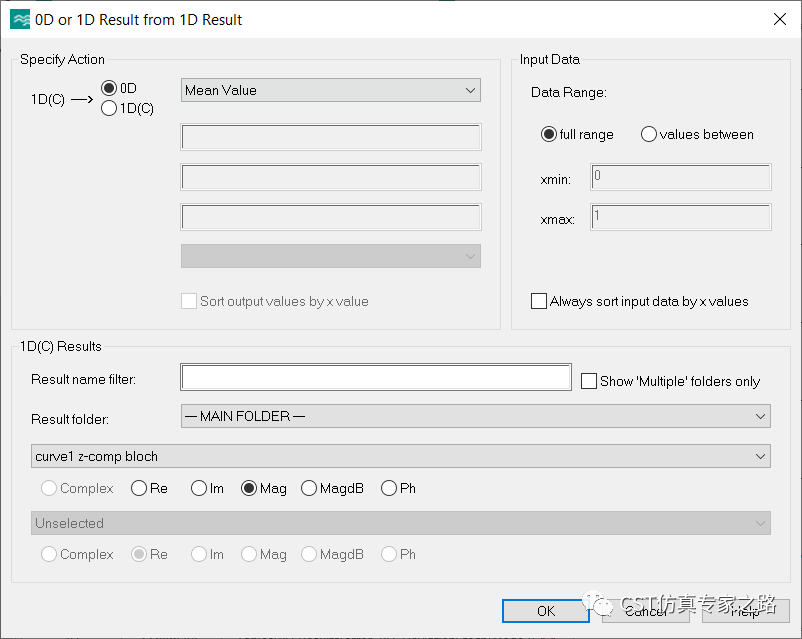
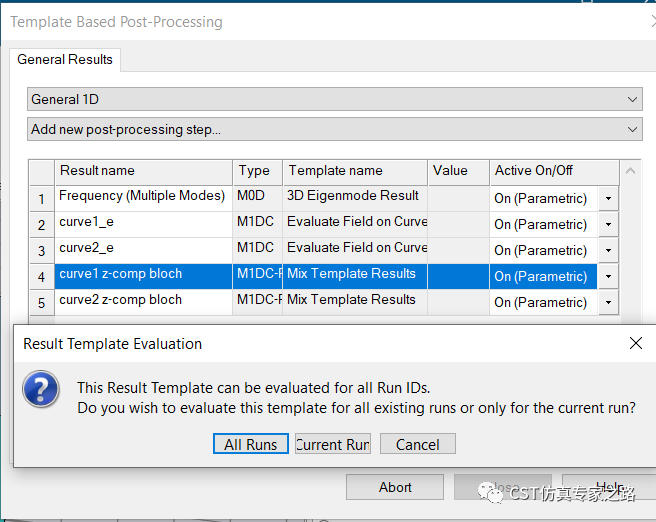
有了两个Curve之后,后处理分别对两个Curve提取Z方向每个模式的电场:
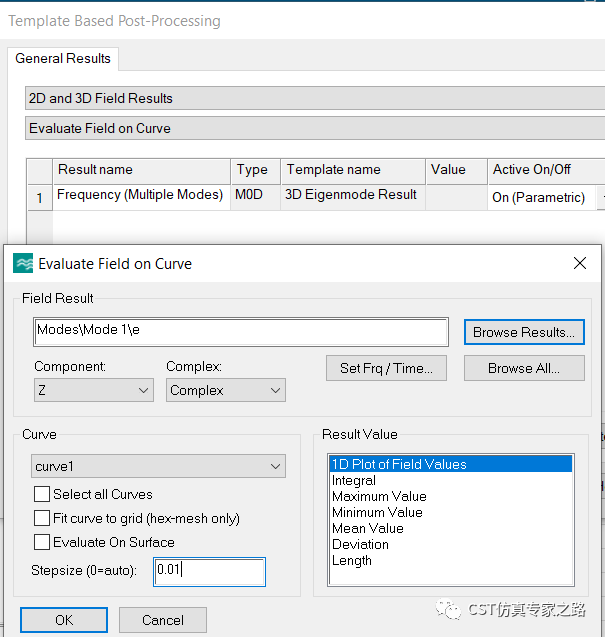
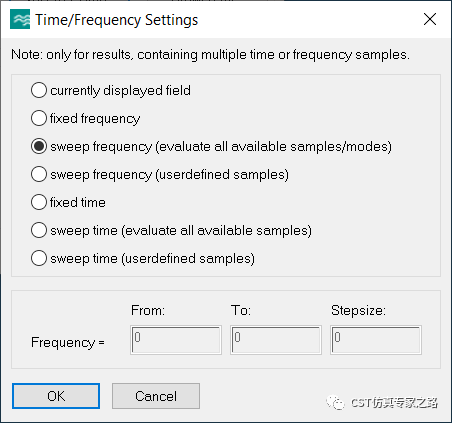
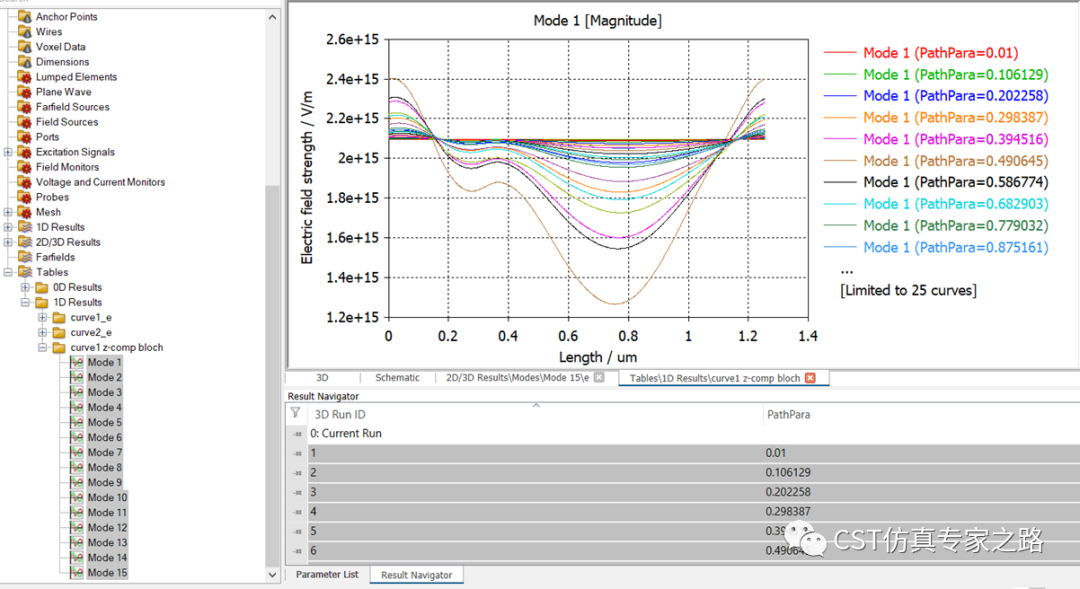
由于参数扫描并没有记录全部的电场,这里可能需要重新参数扫描。结果如下:
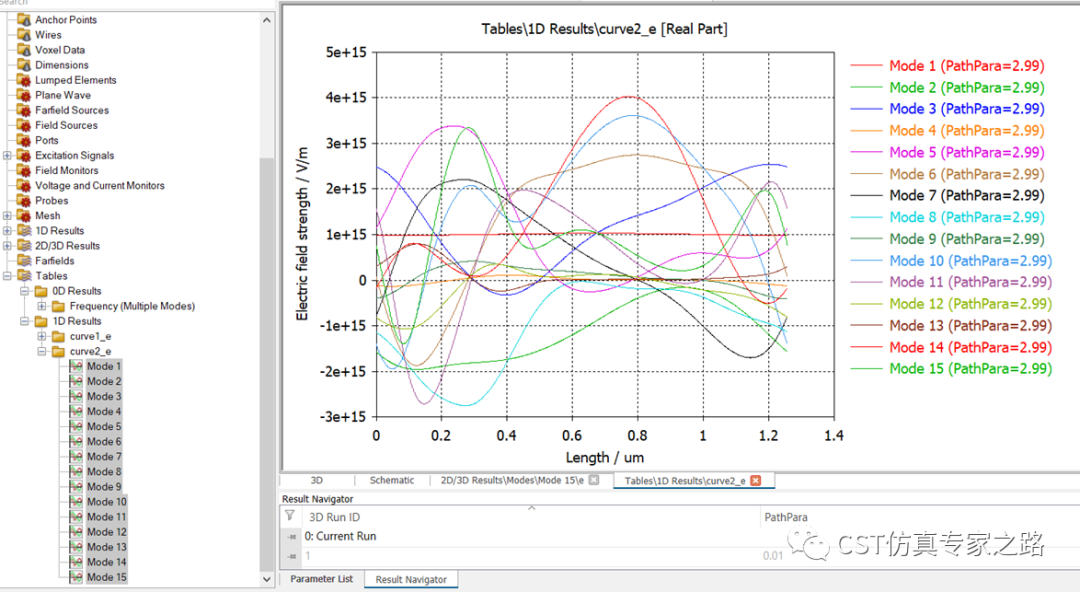
圆曲线的长度定义是从X+方向为0,逆时针转的。不确定的话可以对比三维的场强变化来确认长度定义。
下面将电场与反向平面波相位因子相乘,得到curve1的周期函数表达式:
公式用到的向量关系如下:
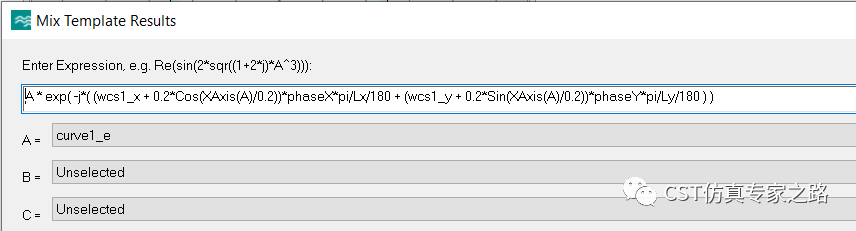
分别计算两个curve上的周期函数表达式:
这个MixTemplate可以不用重新参数扫描,结果如下:
然后curve1的周期式减去curve2 的周期式得到误差值:
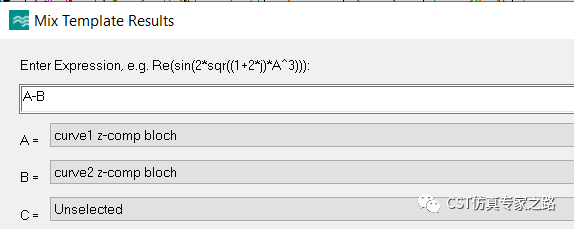
由于数据都是离散采样点,所以要用Stochastic的方法计算标准差:这里取实部就可以了,因为我们最后只需要一组实数来做决定,通过或不通过之前计算的这些Mode值而已。并且,这里如果选Mag, 并不能给我们有效的信息,因为相同的Mag,也可以是不同的实部虚部。
所以在这一步,数据类型正式从电场复数变成实数(1DC变0D)。
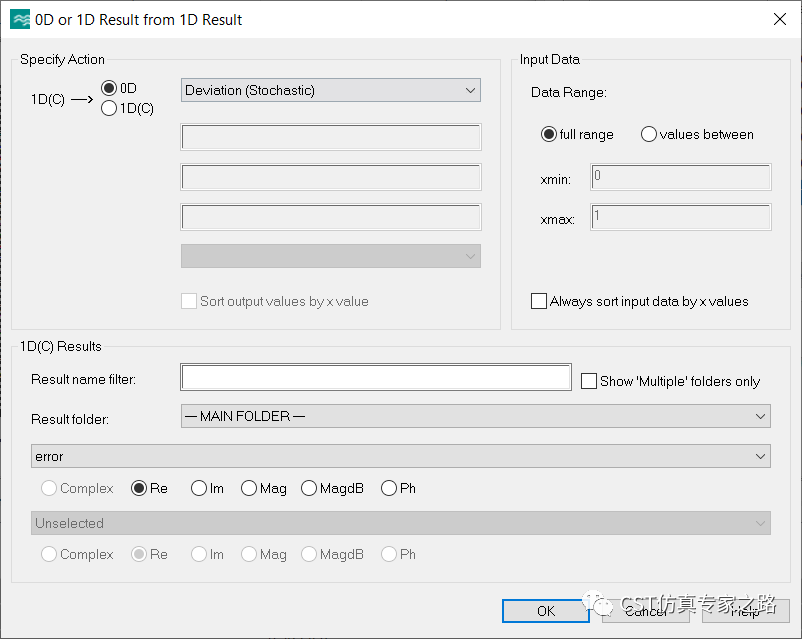
标准差值如下,其实这里就可以看出一些我们想要的结果了,就是近乎0值的这些区域说明就是满足周期函数。
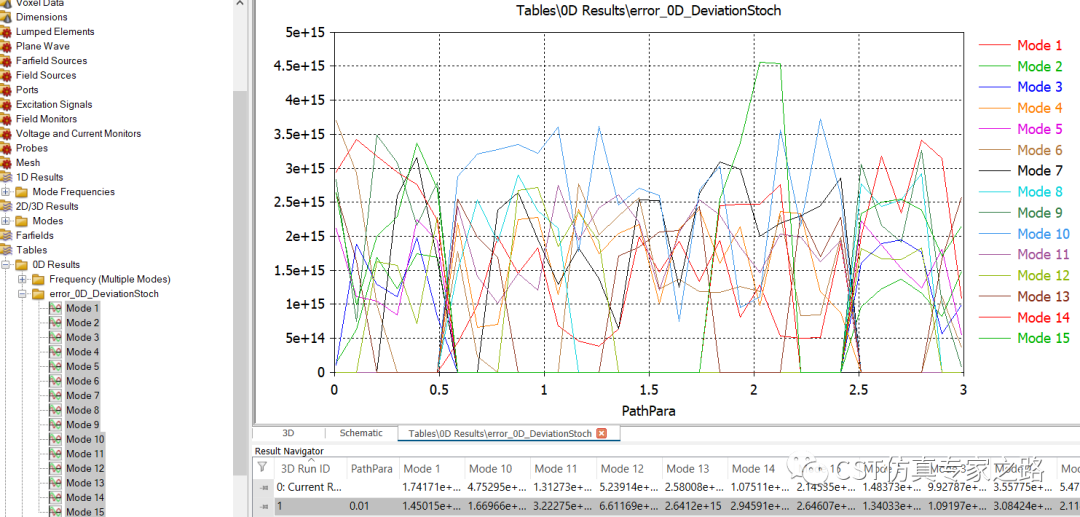
为了得到通过或不通过这样的二进制数据,我们用标准差除以curve1的幅度平均值,得到变异系数:

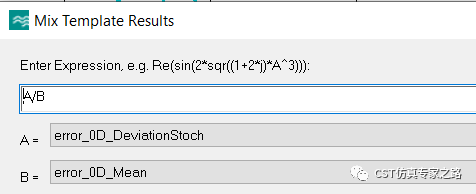
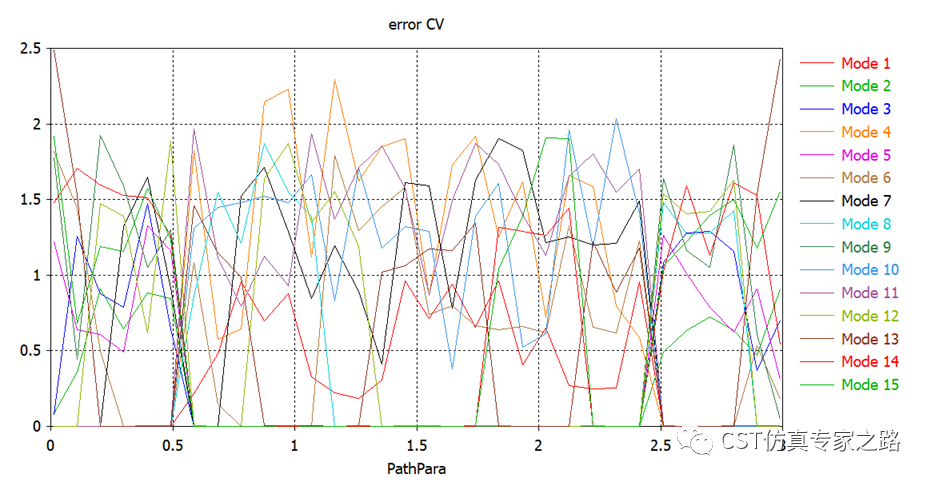
选取变异系数小于0.05的参数PathPara为1,其他为0:
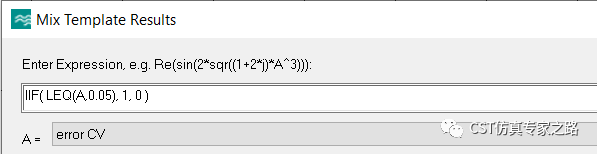
将结果与之前的色散图相乘,获得新的色散图:

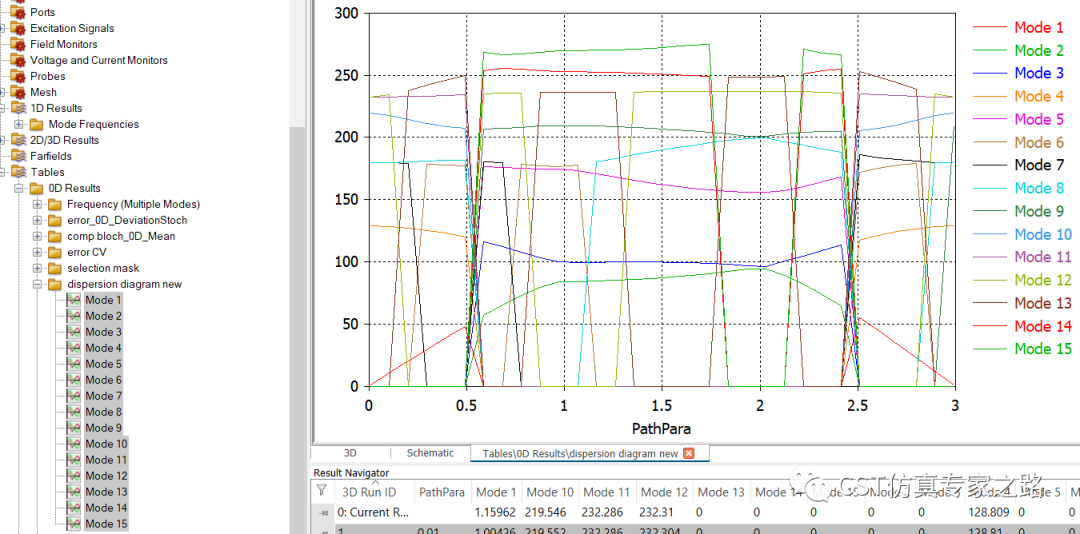
调整曲线为相同的点:

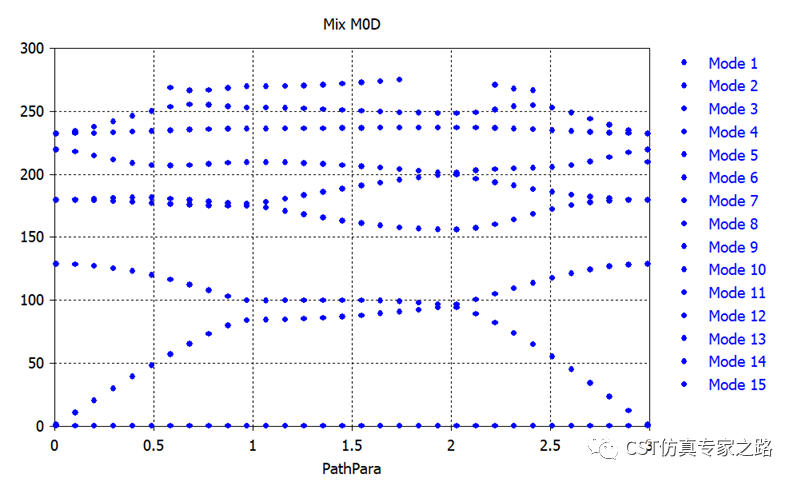
可将Y轴归一化,晶格周期是1um:
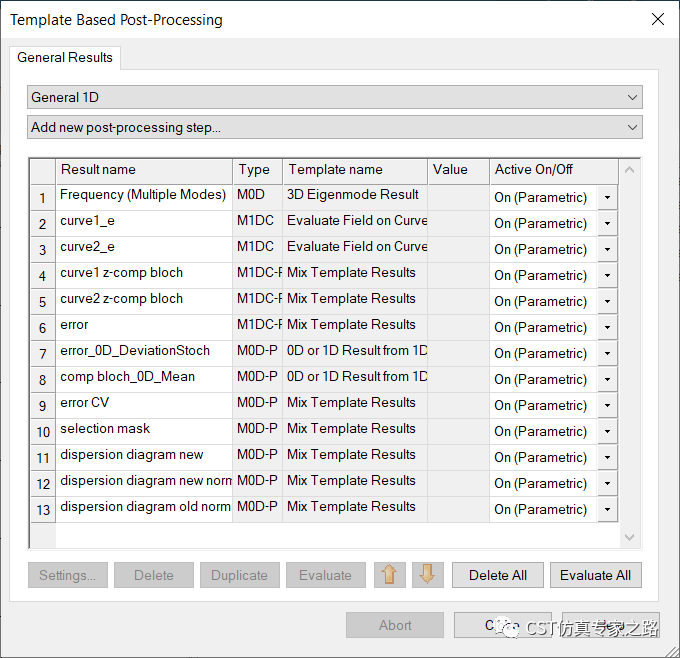
全部的后处理:
将新旧色散图放一起,可见真正的TM模式被标注出来:
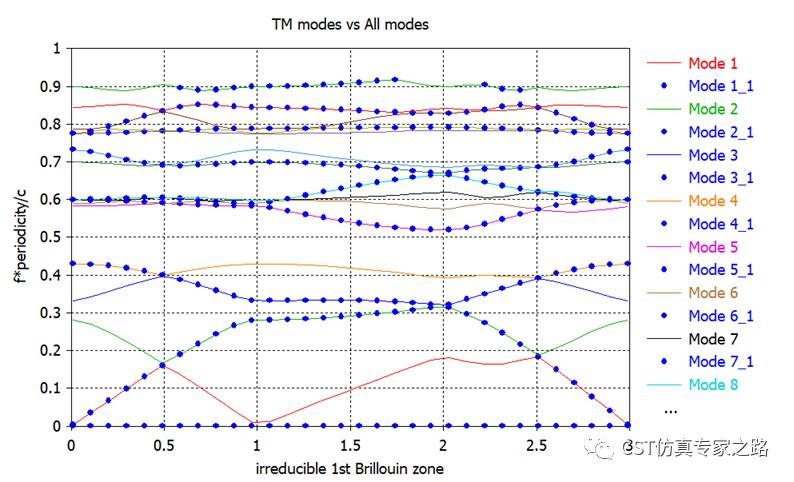
结果与文献中的TM模式一致:
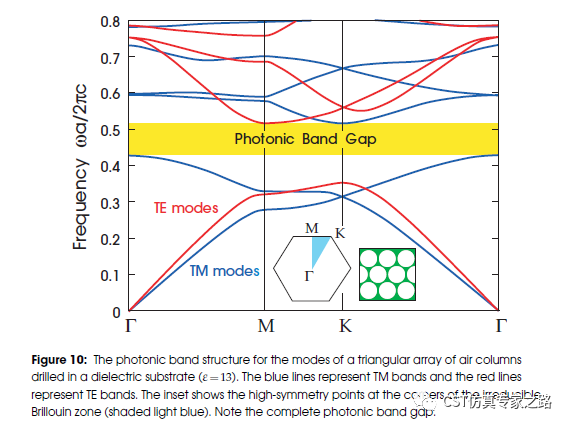
参考文献:
J.D. Joannopoulos, “Photonic Crystals:Molding the Flow of Light”, Chap. 5
小结:
1) 文中的模式式TM,如果要看TE,边界要改成Magnetic,curve上要看Z磁场。完整的能级分析需要TE和TM。
2) 可能有人好奇,为什么要看圆型curve呢?其他curve行不行?我觉得理论上可以,不过圆形上的点坐标容易写,sin和cos就行,圈定的区域也比较有代表性。
3) 本文还用了一些统计学的手段,研究两组数据的重叠情况。
4) 60度角的晶格需要我们调整布里渊区,就是CST中的ParaPath参数定义式,文中是90度的XY,以后我们会写关于60度的XY以及更容易获得布洛赫模的方法。
5) 手动验证布洛赫定理公式成功~ 手动虽复杂,但是可以学的更多~





