直角反射器CST仿真实例（2）- 距离分辨率，ICZT与逆傅里叶IFT

上期写了用Field sources模式和ICZT算法来计算一维距离像，物体只是一个，所以很容易分辨出来。

这期我们用同样的案例，物体是两个，看看如何分辨距离，还有ICZT与IFT的对比。 

先通过transform复制直角反射器，使径向的距离相差20mm：     

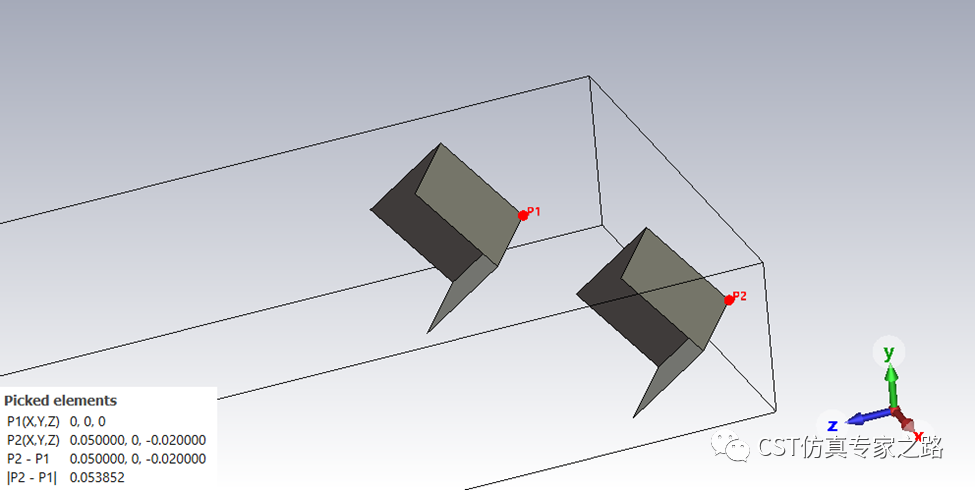
场源距离两个物体是2m和2.02m。

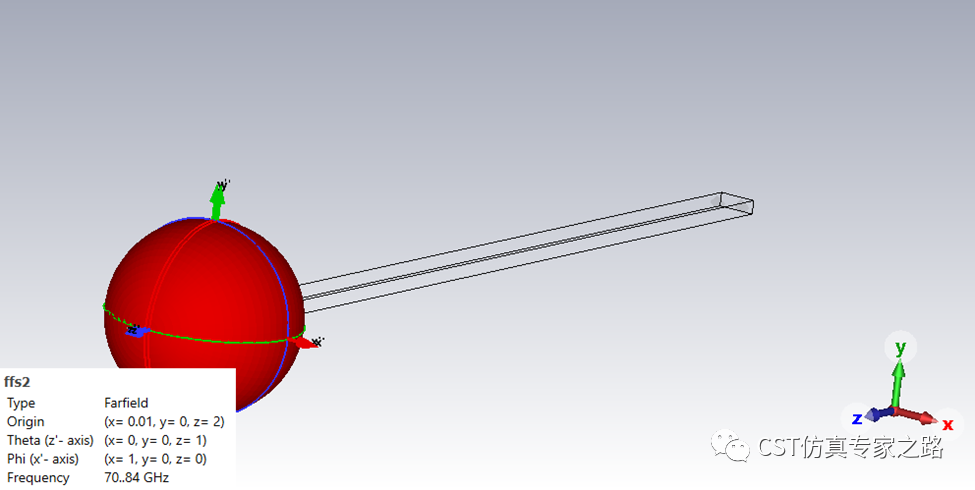
A求解器还是计算的宽频，频域采样间距Fstep=0.0125还是满足奈奎斯特条件和我们Tmax=20ns的假设： 

  计算F21 (antenna coupling)，开始仿真：

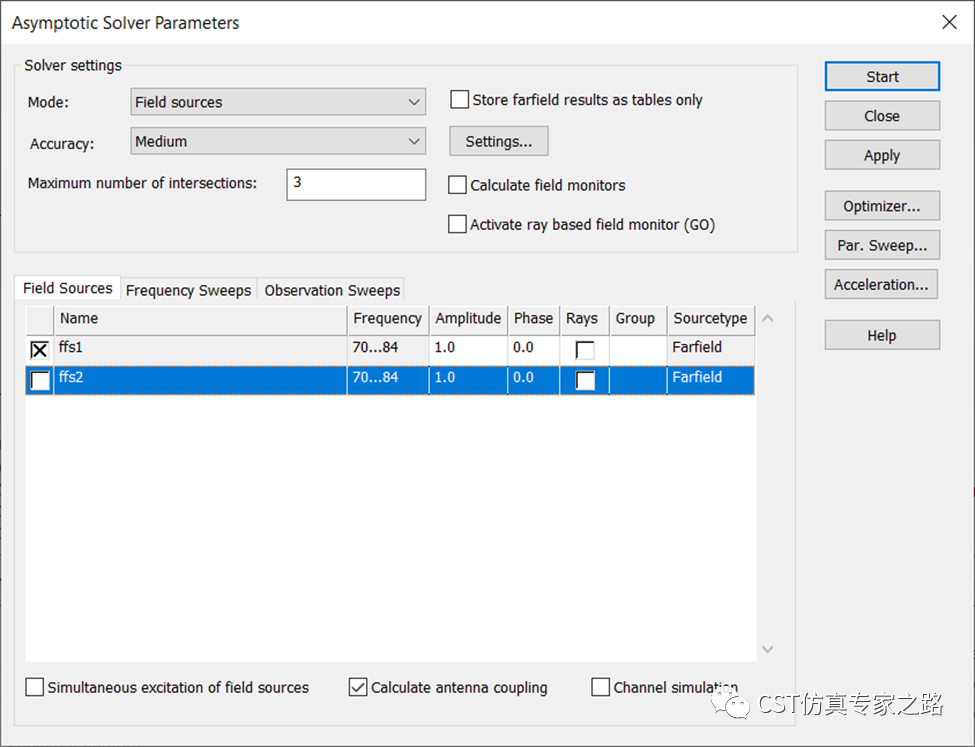
同样使用逆ChirpZ变换的后处理，我们将求解器计算的全部带宽14GHz都用上，结果也只是一个波峰，分辨不出两个物体：

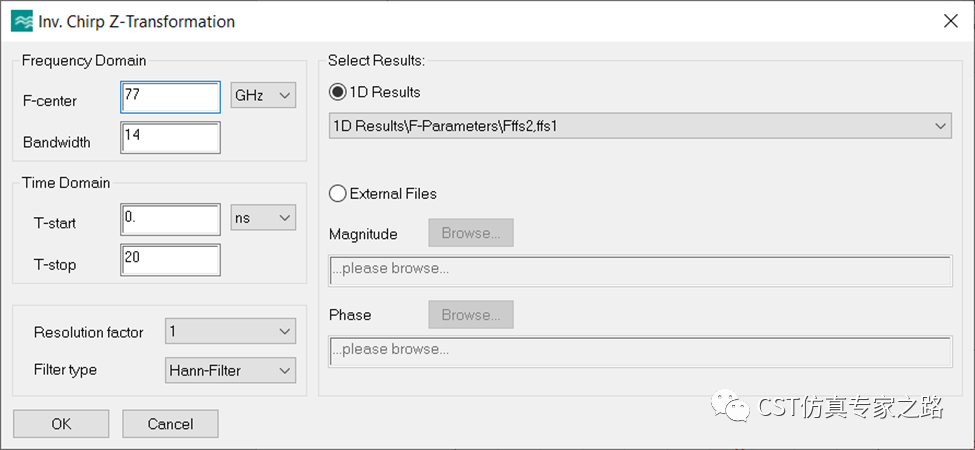
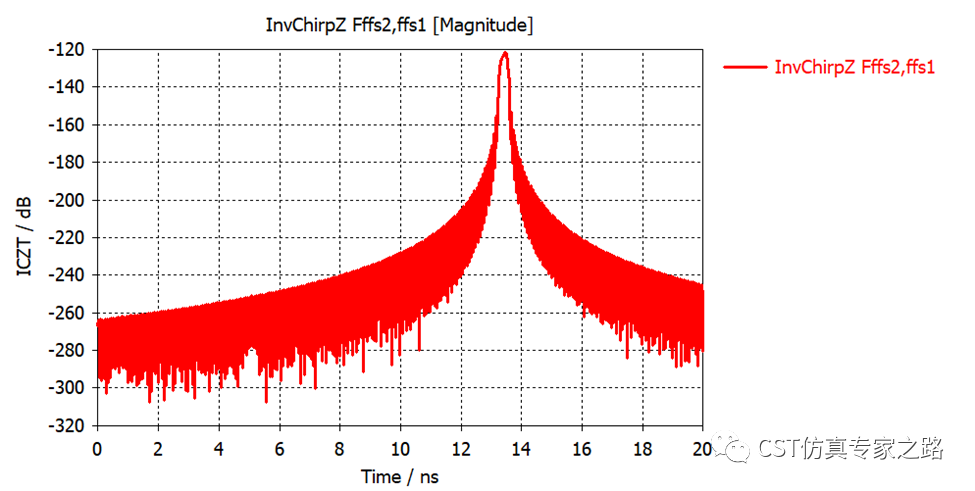
这里横坐标是时域结果，我就不换成距离像了。可以简单验证：峰值13.4ns是往返时间，所以测得的物体距离是13.4/2*1e-9*3e8=2.01m左右。

那么我们现在的距离分辨率是多少呢？dR=CLight/Bandwidth/2, 所以距离分辨率目前是3e8/14e9/2=0.01m，也就是说，2.01+/-0.01m的范围内有物体，所以分辨不出来2m和2.02m的两个物体了（两个波峰几乎重合了）。

那么如何分辨出这0.02m的差别呢？当然是增加带宽，可我们这里用的的远场源当初定义的时候就只包括70-84GHz的带宽，所以增加带宽是不行了。为了演示分辨两个物体，我们可以将径向间距扩大到0.04m，这样14GHz带宽是可以区分两个物体的：

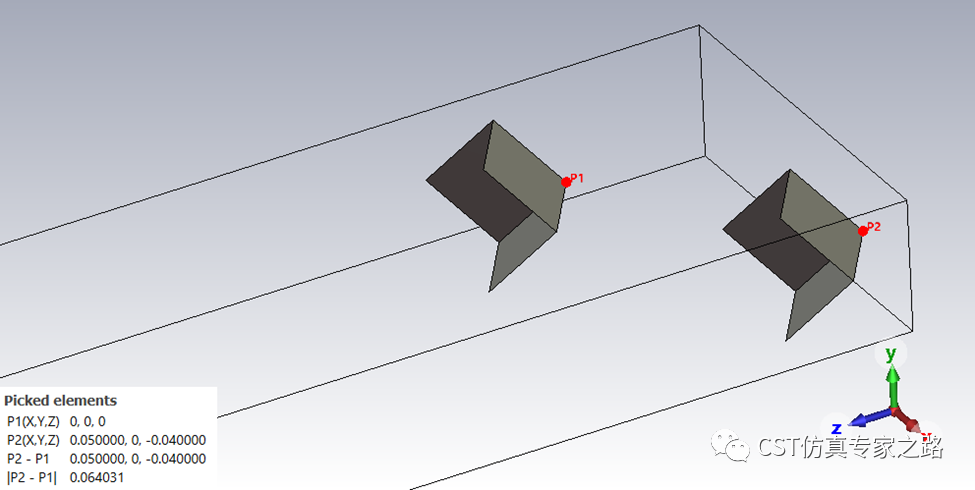
重新开始仿真，自动运行后处理，用的还是14GHz带宽和Tmax，这种情况我们就可以用两个波峰分辨两个距离了：

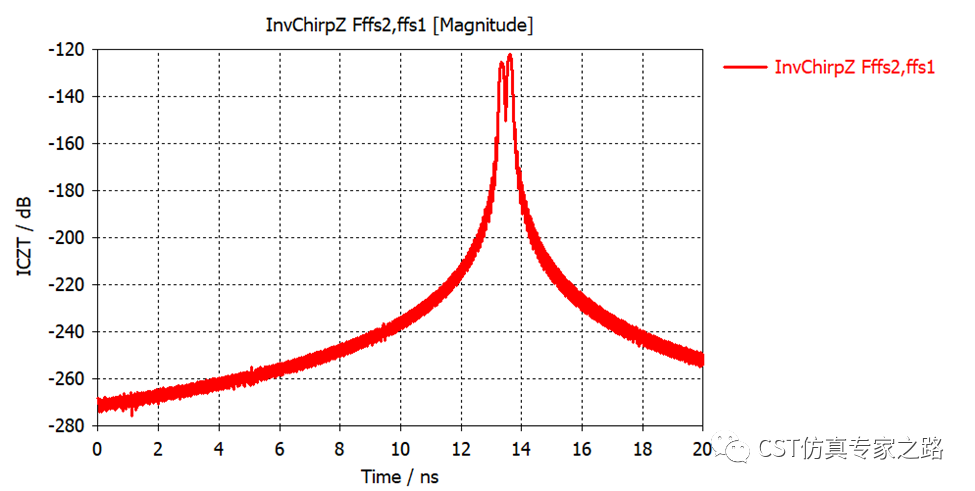
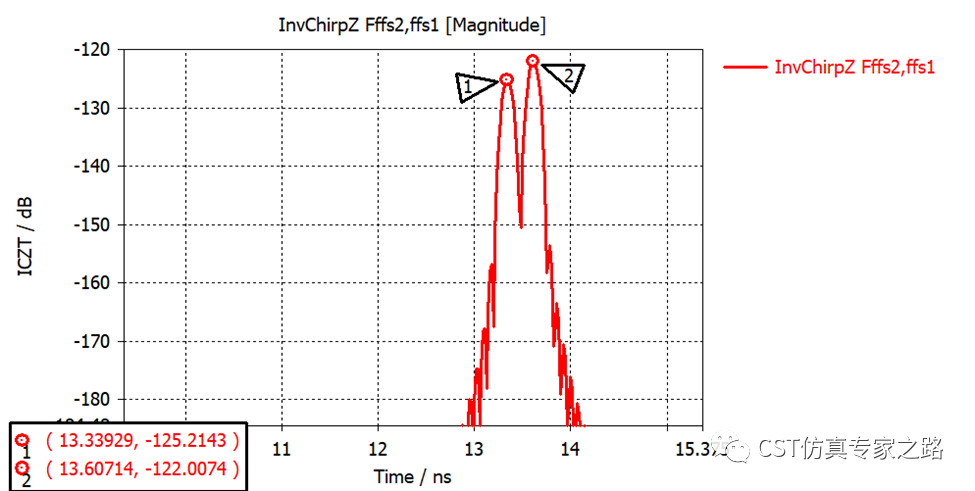
可以验证一下两个时域波峰时差和0.04m距离差的关系：0.268/2*1e-9*3e8=0.04m，没错。 

下面我们用逆傅里叶IFT验证一下为什么我们设置的Fstep=0.0125GHz在这里满足奈奎斯特条件。上期提到过，假如我们的时域信号最大看到20ns，那么最小采样密度df=1/2/20ns，最大频率的最少采样数为2*84G/df= 6720个，进入傅里叶变换后处理：

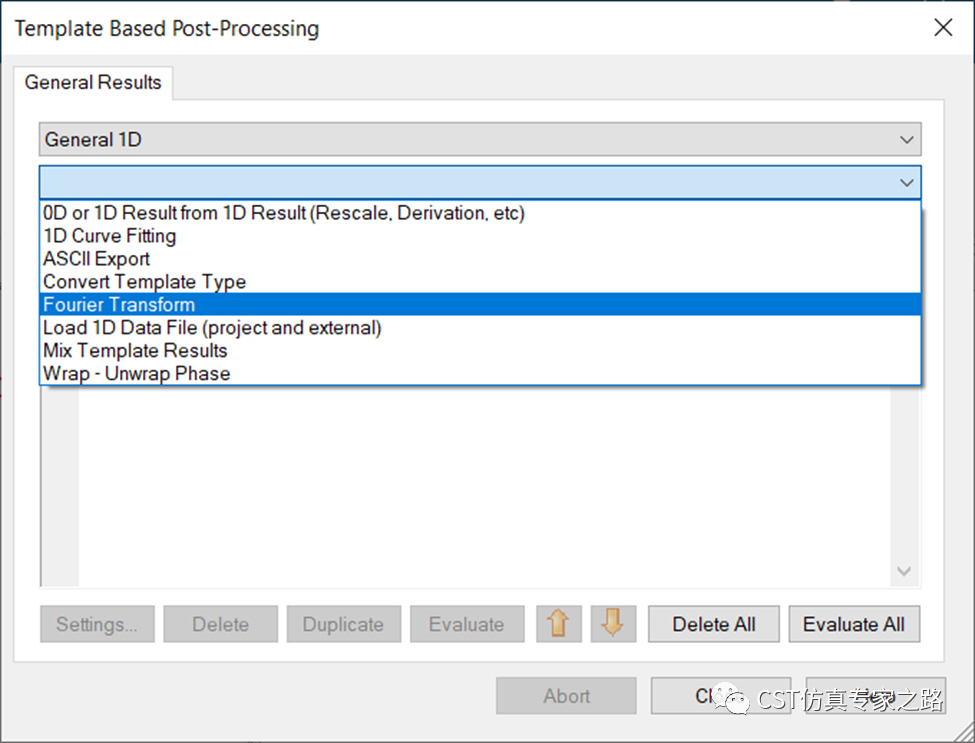
对F21进行IFT计算，最大时间同样是20ns，选择Nyquist重新采样，如果我们用同样的采样数6720, 则计算顺利：

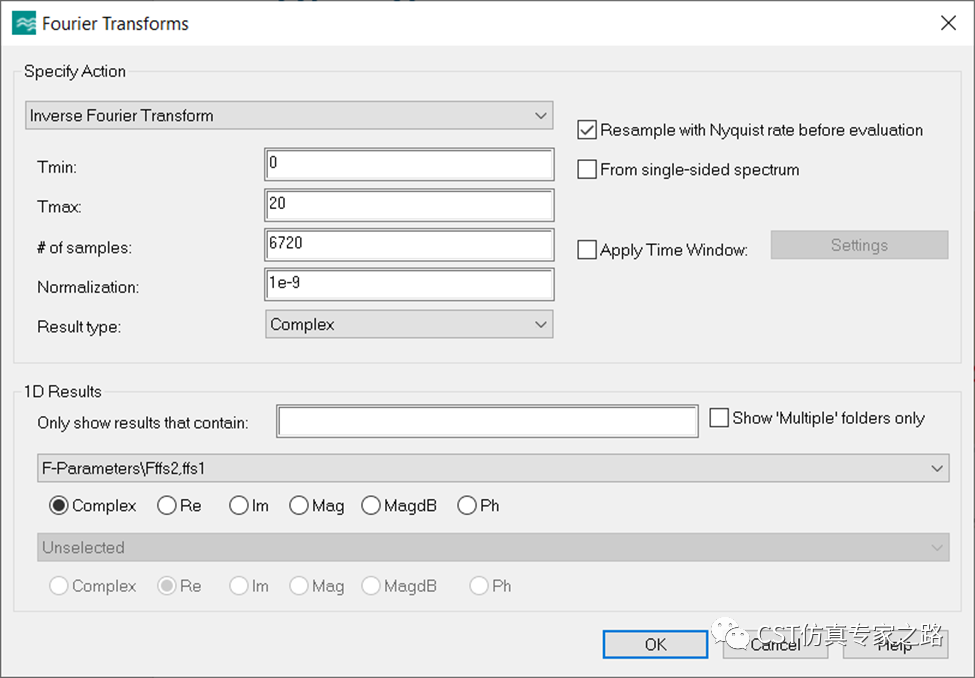
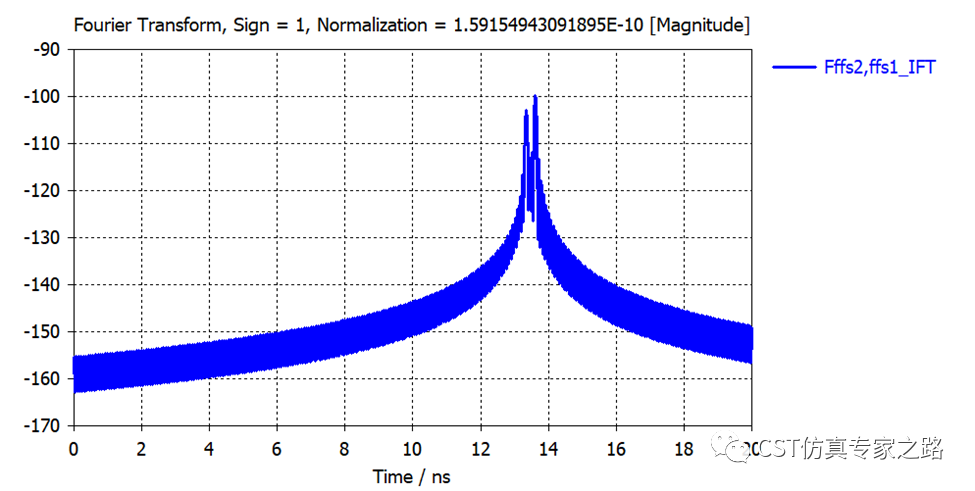
这里IFT虽然也能看出两个波峰，但功能上不如ICZT，这个结果也不能完全和ICZT相比，所以我们就不放在一起了，算法还是有差别的。

若少一点IFT采样，则提示采样不够：

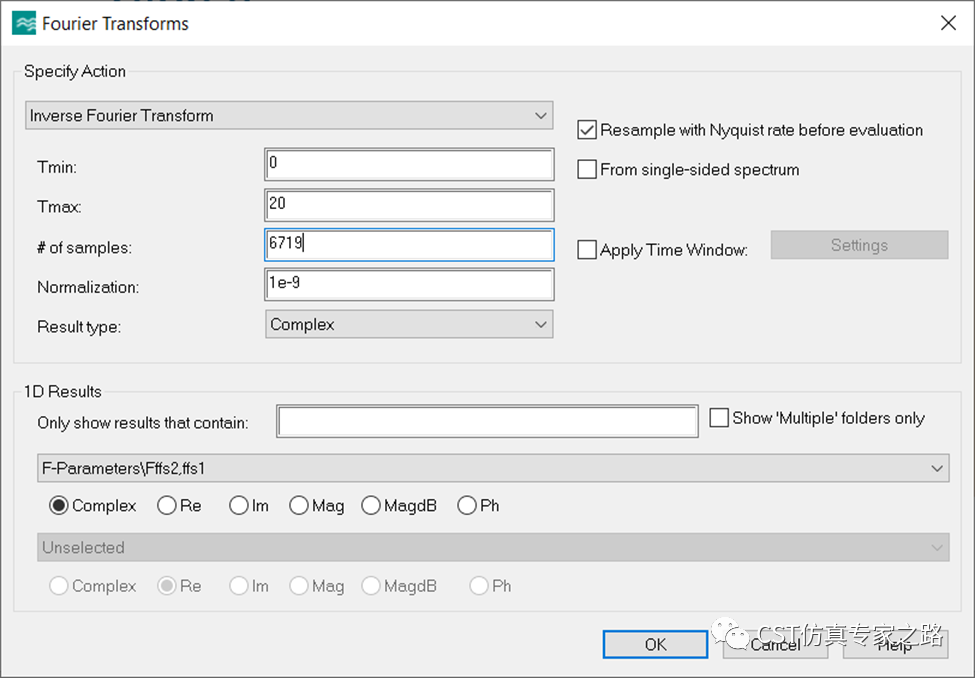
小结：

1）场源带宽和求解器带宽可以设置相同，这个是仿真项目能用到的最大带宽；后处理进行ICZT时，可用最大带宽内的任意带宽。

2）距离分辨率只受带宽影响：dR=CLight/Bandwidth/2。有的表达式也写成Rres=c/BW之类的，若不除以2，可能是往返距离。

3）IFT只用来验证ICZT的采样，不能替代ICZT计算距离像。ICZT模板有更多功能，比如设置带宽、滤波器以及补零功能等等，ICZT配合A求解器中的Nyquist采样，更适合用来手动计算距离像。

4）A求解器中的频域采样数太多会减慢计算速度，收益也不大，所以要按Nyquist设置比较好。