CST激励源之波导端口(1)
波导端口是一种特殊种类的解算域边界条件,它可以刺激能量的吸收,这一切都是是通 过2D频域解算器求解二维端口面内可能本征模实现的,且端口处每种可能的电磁场解析解都可以通过无数模式的叠加求得,然而,实际上,少量的模式就可以进行场仿真了,求解计 算中需要考虑的模式数可以在WaveguidePort对话框中设定。
这里要注意:激励波导端口的输入信号是规一化到峰值功率为1sqrt(Watt)使用波导端口要根据不同需求、不同特点的端口类型的数量定义。因而,我们首先必须
精确的判定激励问题的类型,然后在选择并定义合适的波导端口。在具有不均匀性、可获得 broadbandports(宽带端口)或者具有inhomogeneousportaccuracyenhancement(非均匀端口精度加密)特色的情况下,我们可以选择使用normal waveguide ports(标准波导端口), 与此同时,multipinports可以计算凋落的TEM模。
标准波导端口标准波导端口即我们经常使用的矩形或圆形波导结构,通过PEC边界条件屏蔽,因而端口模式就被限制在端口区域内均匀波导端口;如下图是一个均匀、矩形标准波导端口,通过 normal waveguide operator 解算。下图中是一个具有三个模式 的波导端口,这里按各自的截止频率来分类。传播模式 数的多少取决于选取的频率范围。在瞬态仿真时,建议 考虑所有的传播模式,因为未考虑的模式将在端口处引 起反射。对于凋落模式也采用同样的考虑,如果必要的 话,求解器将检查这些情况并给出警告信息。
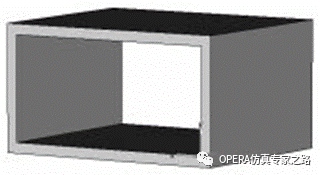

非均匀波导端口如果波导由两种或两种以上材料的介质填充如下图所示,
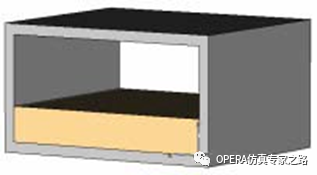
那么模式就呈现频率依赖性,如下图所示就是三个不同频点的 TE 模,频率越高(从左到右频率逐渐增加),那么场就更加集 中在具有高介电常数值的材料中(图中浅褐色部分所示)。

因为标准的波导解算器只计算指定频点处的场模式,对于宽带内计算场模式将会报错。因此我们需要打开瞬态解算器中Special对话框(如下图所示)。
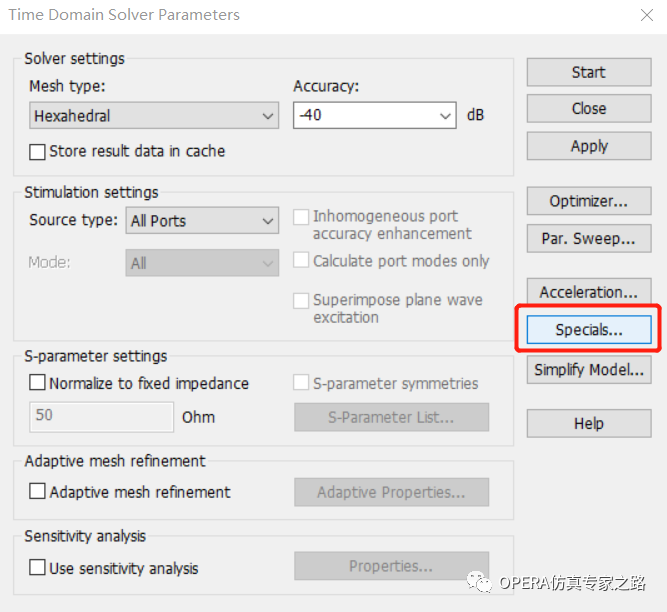
激活其中的broadband port operator(宽带端口解算器),这里,端口模式将在多个频 点处计算并求解出可以接受的宽带结果。
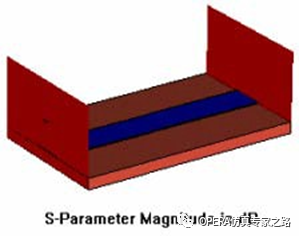
同轴波导端口或连接器和上面的波导端口相比,同轴端口或连接器拥有一个或更多的内导体。在端口处如果存在一个以上的内导体将产生截止频率为0的TEM模。右图中的均匀同轴波导由一个外导体和四个内导体构成,因此存在三 个不同TEM模式,如下图所示。这些模式是凋落模(具有相同的传播常数),且可以叠加产生新的模式,这是因为他们彼此是正交的。因 此,下图所示的模式解仅仅是一种可能解,因而我们建议你使用 multipinoperator功能指定你期望激励的模式。

非均匀同轴波导或连接器端口假定为轻微不均匀同轴波导或同轴连接器端口,通过使用MultipinPort,依旧会叠加产生许多QTEM模,然而,切记:不同模式的的传播常数是不同的,这将产生错误信息。假定不均匀错误已经不能忽略调,那么所有的端口应该定义为Single-ended,在仿真结束后,single-ended S参数将作为后处理中一部分,然后在CST DESIGN STUDIO中通过类似结构的multipin配置的微分激励重新合并计算。
微带线不像同轴波或矩形波导,微带线是开放且不均匀结构,这使得在时域仿真中受到一定的限制。然而,为了获取更精确的结果,我们应该考虑下面的几个方面:
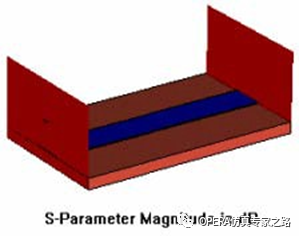
首先,在2D本征模计算中没有开放边界条件,基于此,时域中的开放边界条件则被2D 本征模计算中的磁边界条件取代。因此,为改善精度在远区对重要的模式场尽可能的设置边 界条件是很重要的。由于端口的跳变,高次模就有可能产生,从而降低求解精度。其次,由于端口区域的不连续性,波导解算器waveguideoperator增加了模式计算次数以及距离从而降低了精度,同时发生的宽带错误也可能不再使用inhomogeneousportaccuracyenhancement(在瞬态求解对话框中设定)功能,这个特征使用fulldeembedding就需要所有端口模式的激励,因此,慎重的激活该功能是明智的,如果可能的话,可以使用S-parameter symmetries,下面给出微带线的例子,都是基于标准波导端口解算器(normalwaveguideoperator)。单根微带线 右图是一个有两个标准波导端口的简单微带线,下图给出了求得的 S 参数 ,由于 chosen mode calculation Frequency选择模式计算频率,在10GHz左右, 其反射是正确的,作为对比,右图中则给出了使用full deembedding的结果,在整个期望的频率范围内其反射小 于-60dB。
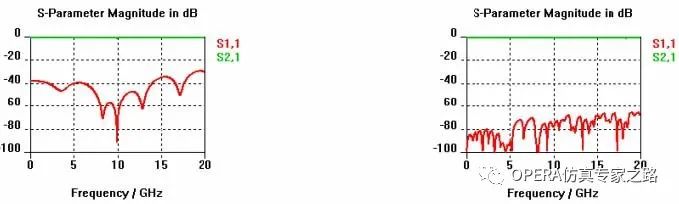
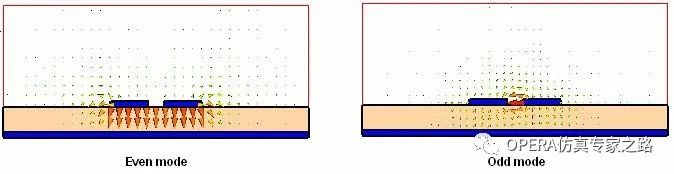
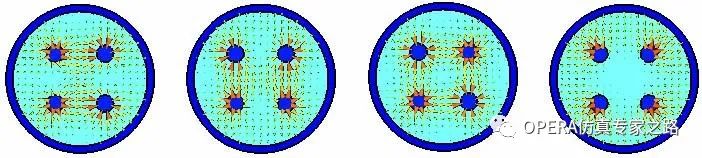
带有接地平面的两个导体微带线下图给出带有接地平面的两个导体微带线的奇模、偶模分布,由于端口区域的不连续性,
其奇偶模都是非退化的QTEM(准TEM波),描绘了这种结构的两种静态模式。