Secondary Electron Emission: Overview

Introduction to Secondary Emission

Furman

Backscattered or elastic reflected electrons

Rediffused electrons

True secondary electrons

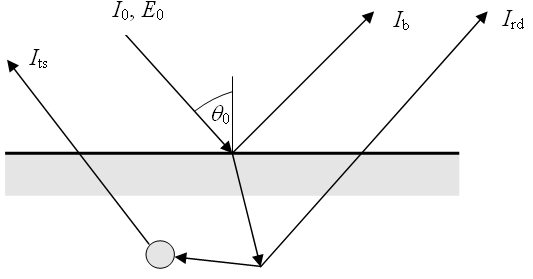
General model assumptions/definitions

Introduction to Secondary Emission

In general, secondary electrons can be generated in three different ways:

Backscattered electrons. An incident electron undergoes an elastic collision at the surface of a material and it is reflected back.
Rediffused electrons. An incident electron moves into a material, but it is scattered back out of the material.
True electrons. An incident electron moves into a material and due to collisions, electrons other than the incident one are scattered out of the material.

The Import and the Vaughan [0] emission model consider only true secondary electrons whereas the Furman [1] emission model considers all three types of secondary electrons mentioned above. Thus the Furman emission model is usually the most accurate emission model, but a lot of parameters must be defined to set up the emission model properly. In many cases the Vaughan or Import emission model is sufficient.

The secondary yield is defined by the ratio of the emitted current over the incident current and can be greater than one without violating the law of energy conservation.

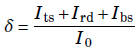
[0] Vaughan: Secondary Emission Formulas.

[1] Furman. Probabilistic model for the simulation of secondary electron emission.

back

Furman Emission Model

Furman: Backscattered or elastic reflected electrons

The probability distribution function (PDF) for the backscattered electrons can be written as follows:

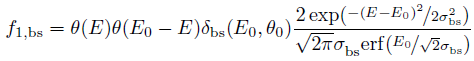
The secondary emission coefficient, which is depended of the incident energy and angle, can be described by:

back

Furman: Rediffused electrons

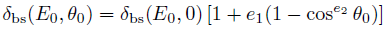
The probability distribution function (PDF) for the rediffused electrons can be written as follows:

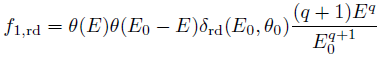
Here, the secondary emission coefficient, which is depended of the incident energy and angle, can be described by:

back

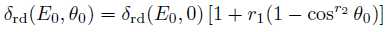
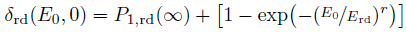
Furman: True secondary electrons

The probability distribution function (PDF) for the true secondary electrons can be written as follows:

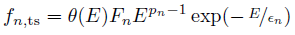
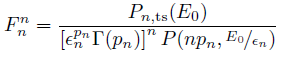
In the above expression, P is the normalized incomplete gamma function. The secondary emission coefficient, which depends on the incident energy and angle, can be described by:

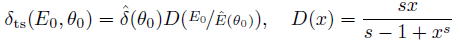
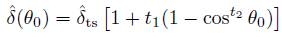
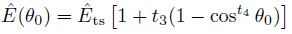
The parameters pn are depend on the material selected via the material dialog tab and they can not be changed by the user.

To avoid the problem that some probabilities can become negative, a modified secondary electron yield is defined:

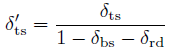
The probability for the true secondary electrons is a binomial distribution, where M is the maximum number of secondary electrons per incident electron:

back

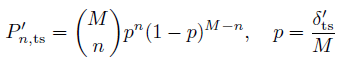
Furman: General model assumptions/definitions

In order to calculate the number of secondary electrons, the probabilities are defined and calculated using the following relationships:

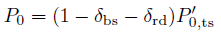
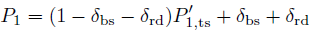
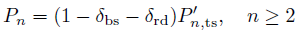
The azimuthal scattering angle is uniformly distributed, whereas the probability distribution function for the polar angle is given by:

back

Vaughan Emission Model

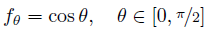
Material Parameters: default - SEE Vaughan

Vaughan: Yield

The Vaughan emission model is a heuristic emission model. The secondary electron yield is defined by three parameters: the threshold energy, the maximum yield and the energy at the maximum yield.

The incident angle theta is included in the model via modifications of the maximum yield and energy according to the following expressions:

and

The parameter ks is a so-called smoothness parameter and depends on the surface of the material. Typically this parameter is set to unity.

To calculate the yield,a normalized incident energy is used, which is defined as follows:

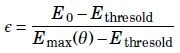
For oblique incident angles, the normalized energy is reduced. Then the following relations hold for the secondary yield as a function of the normalized energy:

back

Vaughan: Energy Distribution

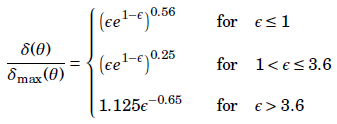
The energy of the secondary particles is gamma distributed. The temperature T is defined by the user. The temperature T is defined in units of energy, eV.

back

Import Emission Model

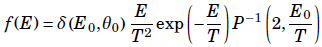
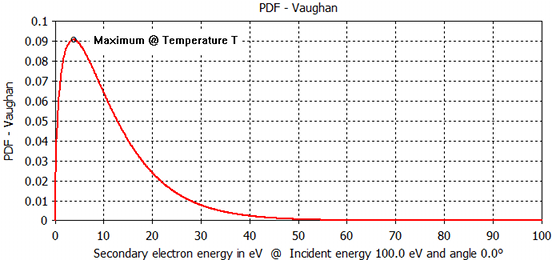
Material Parameters: default - SEE Import

Import: Yield

The secondary electron yield for normal incident (theta = 0) is imported by the user. Thus arbitrary shapes of the SEY curve can be used. The dependency of the incident angle is included via the following relations:

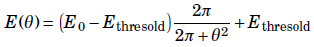
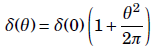
The model is intended to be as simple as possible, thus no surface smoothness is considered. The threshold energy is automatically detected by the import. If the threshold energy is zero, the angular dependency is identical to the dependency in the Vaughan emission model.

back

Import: Energy Distribution

The energy of the secondary particles is follows a gamma distribution. The temperature T can be defined by the user. The temperature T is defined in units of energy, eV.

back

Misc

Deterministic random

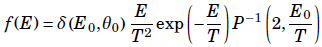
The generation of random numbers for the secondary electron emission is based on a deterministic algorithm, that means calculations are reproducible. If a nondeterministic random number generation process is required, that can be enabled via VBA methods, as shown below for the PIC and tracking solvers. It is noted that two calculations with the same settings and nondeterministic SEE yield different results.

PIC Solver

With PICSolver

.SEEDeterministicRandom "False"

End With

TrackingSolver

With TrackingSolver

.SEEDeterministicRandom "False"

End With

back

Secondary Electron Emission: Overview

Contents

Introduction to Secondary Emission

Furman Emission Model

Vaughan Emission Model

Import Emission Model

Misc