CST分析表面等离子极化激元SPP实例（2）- IMI有效折射率,缝隙波导

表面等离子极化激元SPP发生在金属-介质的表面，所以其实金属或介质都可作为波导的核心。这期我们看一下金属薄膜作为波导。表面等离子体波的波导处于亚波长，在纳米光子领域很有用。对于波导波矢量的表征，有效折射率（effective refrective index）Neff就是最重要的KPI，也叫有效指数或模态指数（modal index）。

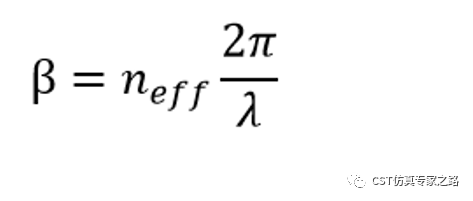
1.    IMI结构等离子体波

先看最基本一种，空气-银-二氧化硅IMI结构（Insulator–metal–insulator）。

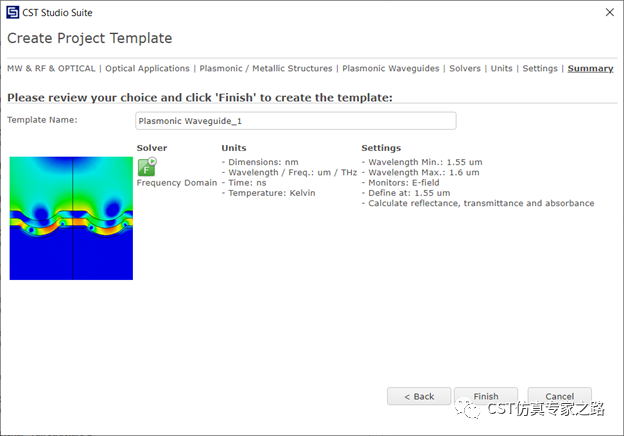
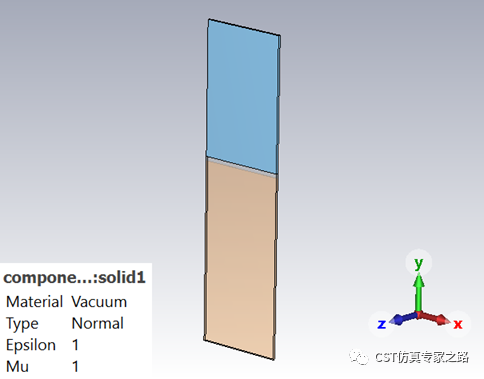
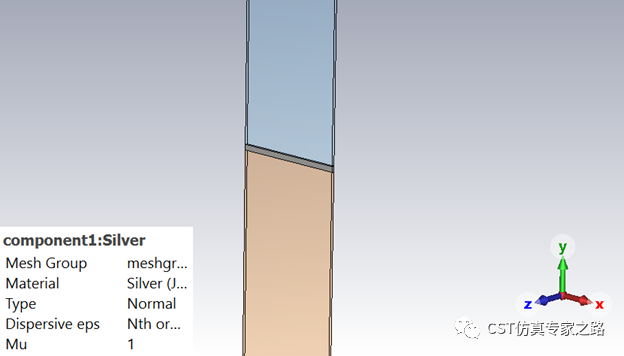
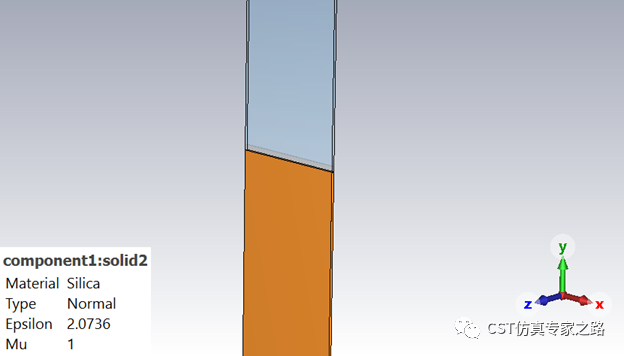
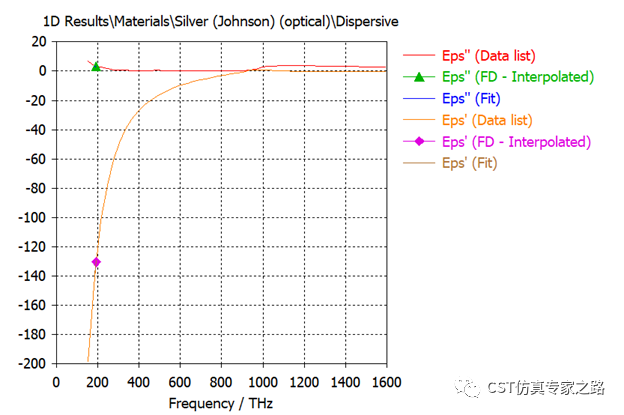
与一般硅光波导不同，这里硅核换成了银，而银在光频的介电为负，所以光不再是集中在波导核心，而是在银和介质交界。 

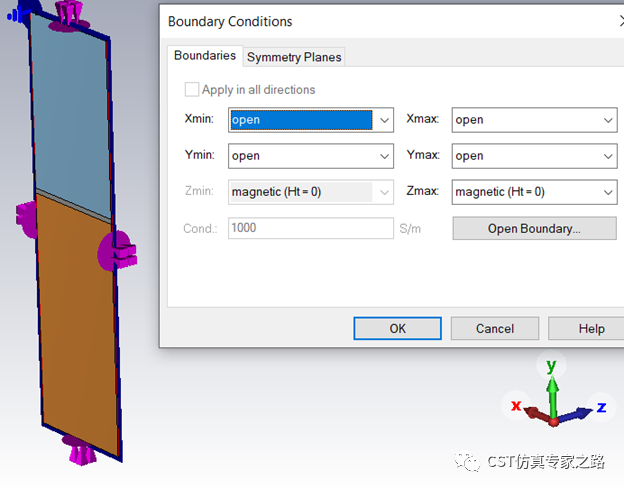
传播方向为X，我们仿真的算是二维的结构，所以端口细长。这种二维的波导我们需要限制两边边界为磁边界，这样TM模式才能激励出SPP。当然实际的波导需要好好设计截面，使模式聚集，而不是用理想磁边界。这里只是为了分析二维SPP模式。 

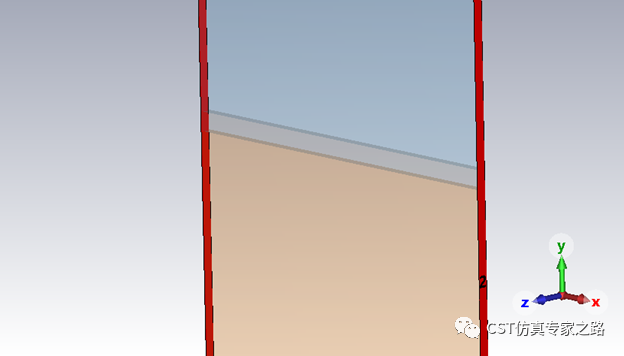
添加后处理计算有效指数： 

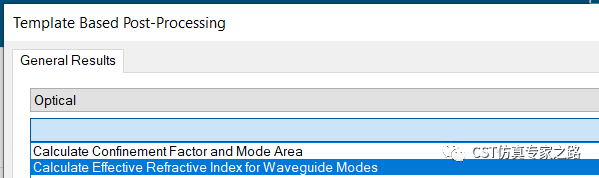
求解器只计算一个频点（波长1.55um）：

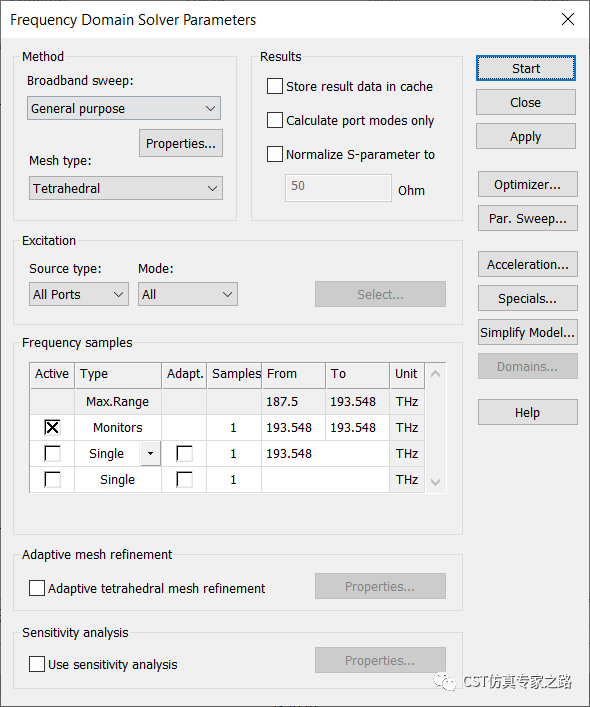
银的高度做个参数扫描，10-100纳米，

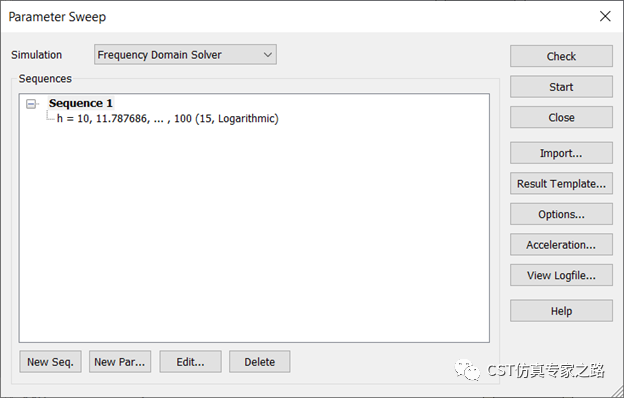
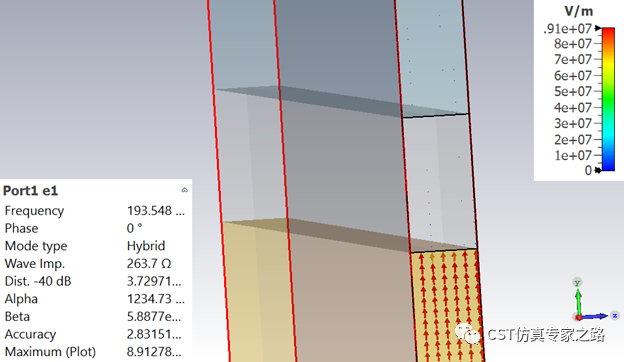
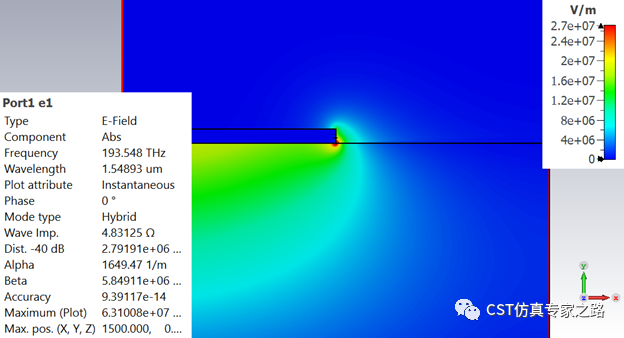
扫描结束后，查看表面等离子波和端口模式（h=100）：

可见2000纳米的长度内差不多接近4个周期，所以我们就按500nm的SPP波长估算，是1550nm的三分之一，远小于空间波长，这就是SPP的SP特性。

电场垂直与交界：

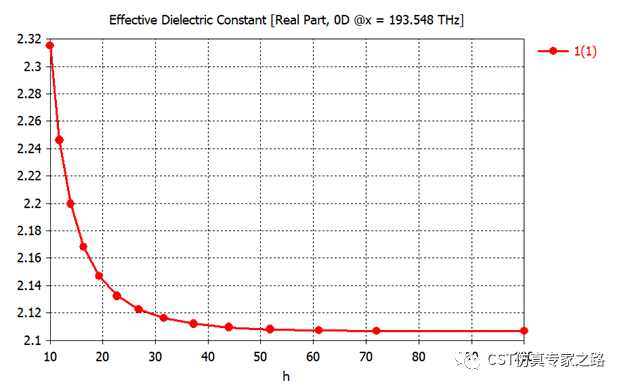
有效折射率随银膜高度变化：

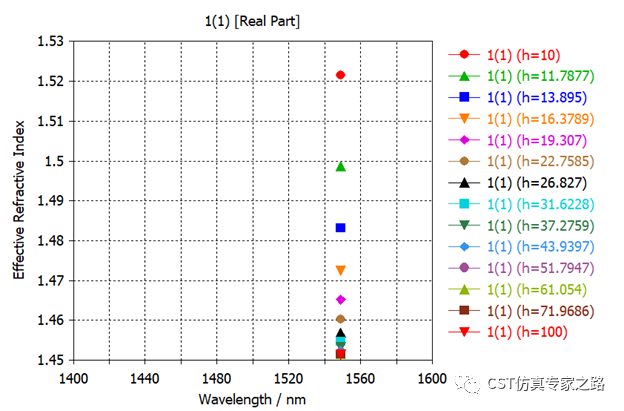
换写成0D结果：

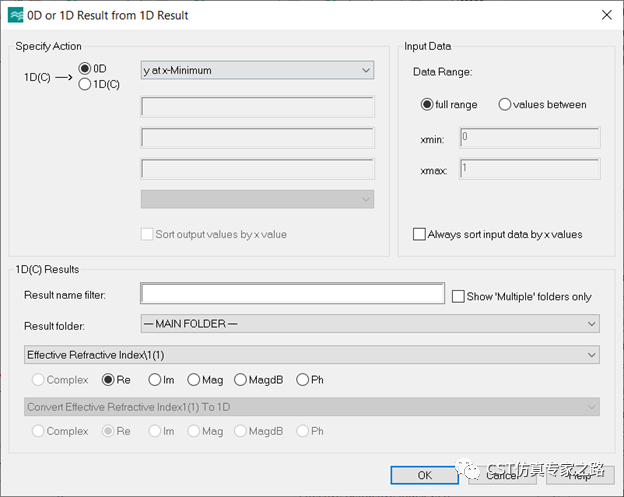
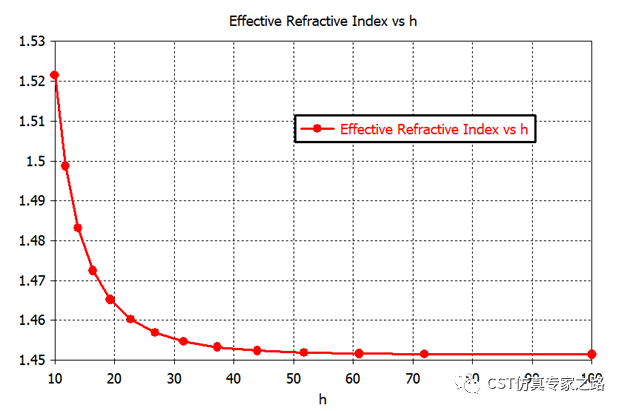
另一种有效指数获取方法是将端口信息中的有效介电常数开根号：

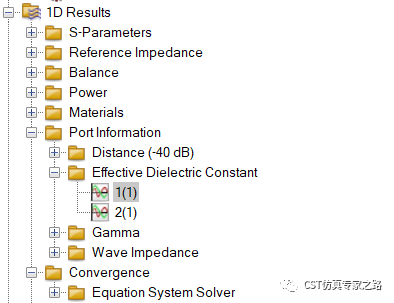
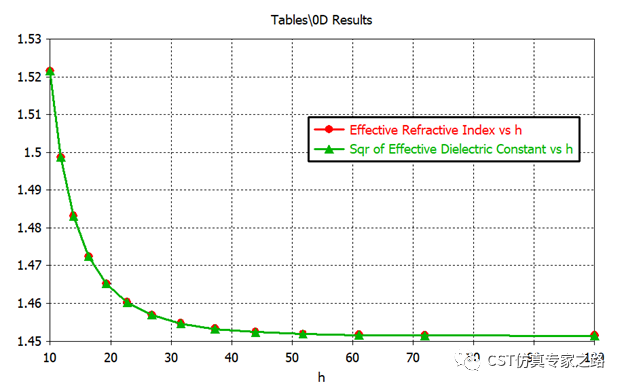
2.    截断IMI结构边界模

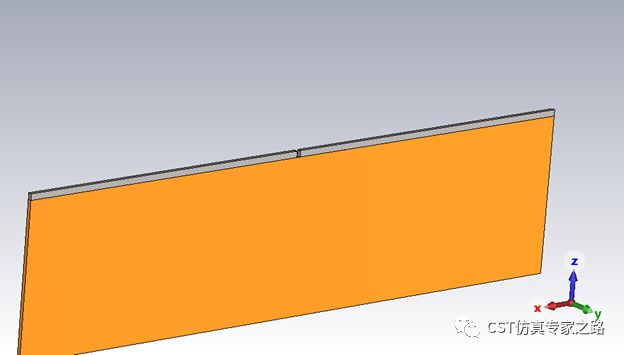
为了形成缝隙波导，截断的IMI结构的边界模式也要分析一下，同样也是获得有效模态指数。注意这里二维结构建模就是截面了，传播方向为Z。 

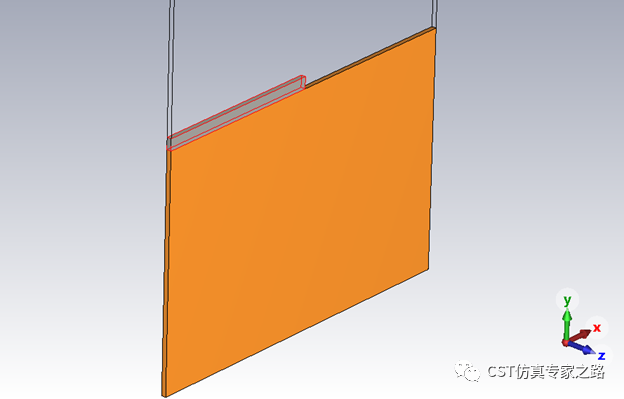
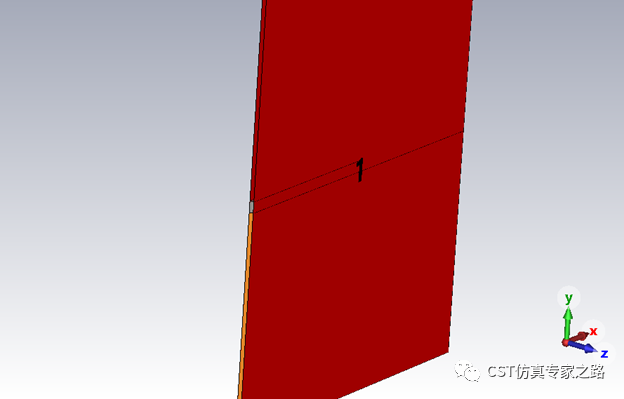
同理可获得有效折射率与银膜高度之间的的曲线，等下一起展示。 

3.    缝隙波导 

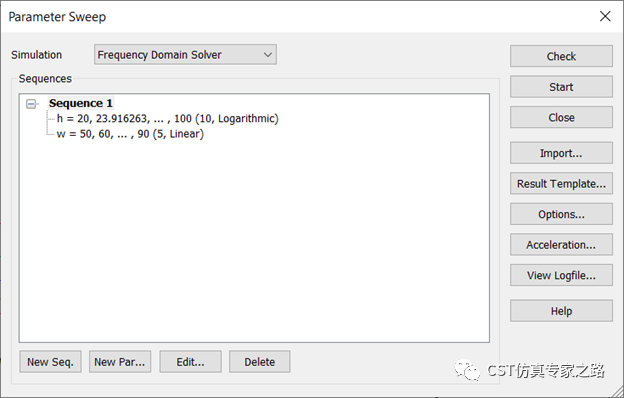
同样也是截面二维建模，参数化缝隙宽带为w，银膜高度为h： 

扫描银的厚度和缝隙的宽度：

可获得每个RunID有效折射率的0D曲线：

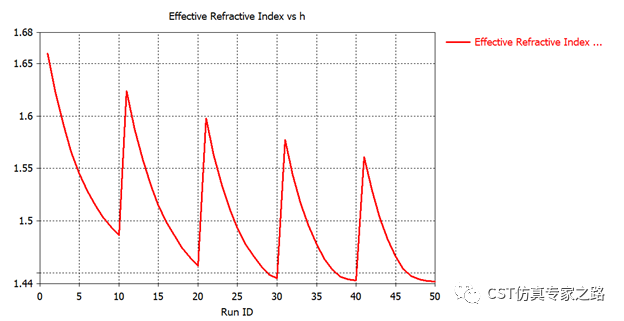
调整数据：

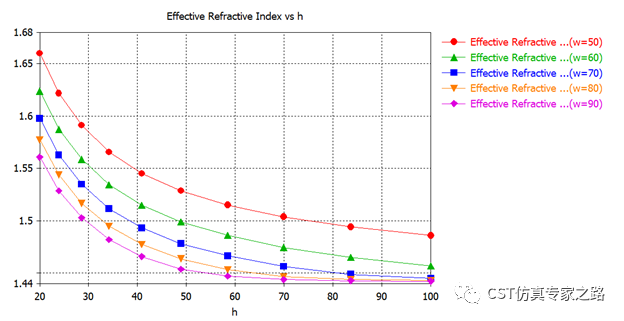
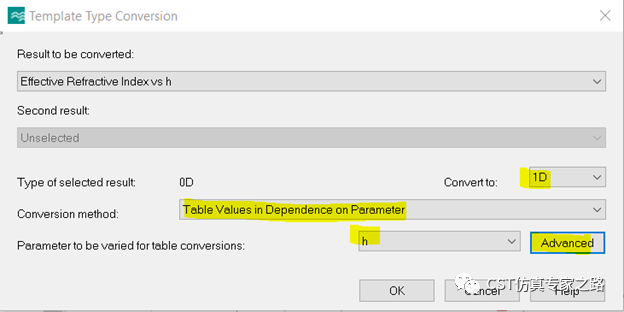
这里也可以通过后处理提取一下每个W的有效折射率曲线，比如w=50：

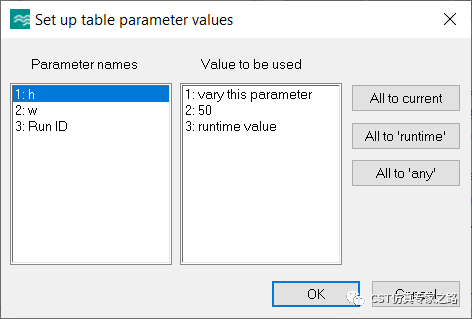
最后，我们把所有的曲线放在一起查看： 

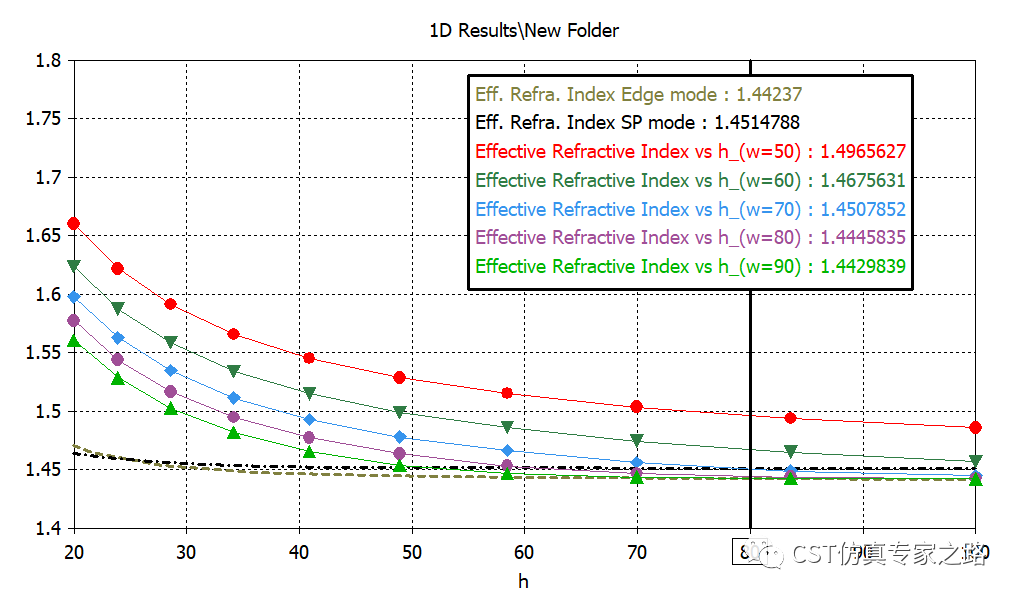
比如在h=80nm时，不同的缝隙宽W的缝隙波导有效指数是可以大于或小于SPP模或边界模的有效指数的。当大于时，波导模式能量聚集，当小于时，有漏波现象：

W=50：

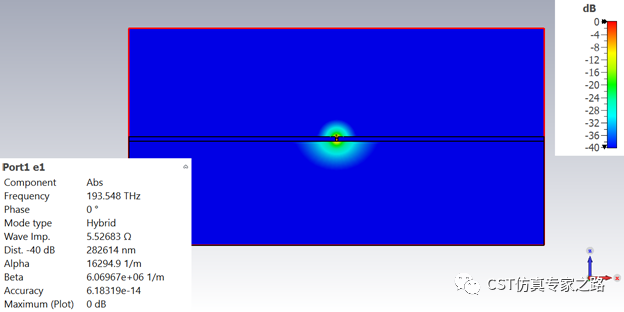
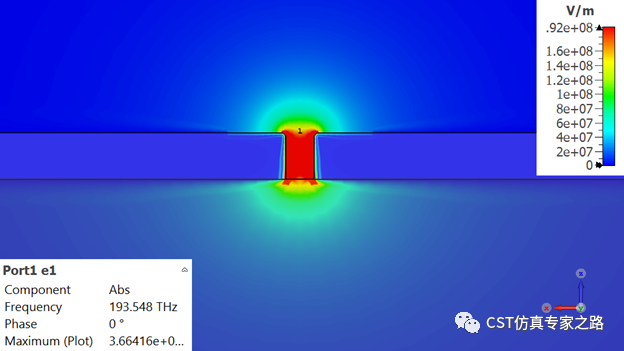
 W=80：

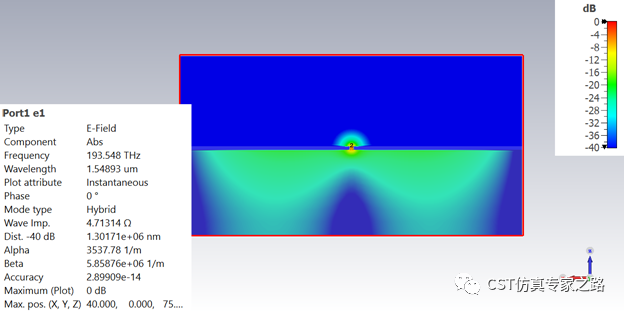
W=200：

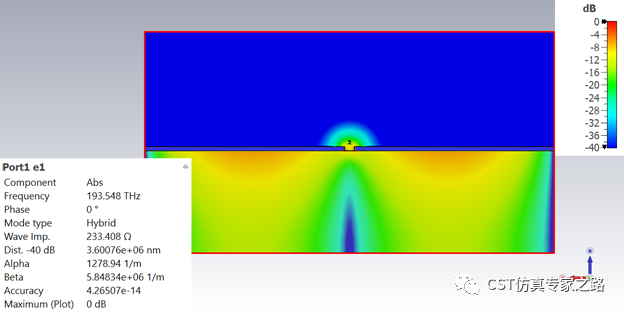
如果还是不清楚这里在仿真什么的话，加长传播方向，展示个表面等离子极化激元的波导传播动图就明白了：

小结：

1.  本案例展示了一些基本的SPP模式仿真，可见最终我们能够用几十纳米尺寸的一个波导，来传播1.55微米的光(严格讲应该是介质中的波长)。这种深亚波长尺寸的应用就是SPP的特点。

2. 光频仿真经常用到二维分析，所谓二维仿真，也就是薄薄一层结构，计算方便。

3. 以上仿真结果与文献一致。

4. 波导仿真13k网格，笔记本电脑仿真一个频点也就半分钟时间。

参考：

Veronis, G., & Fan, S. (2008).Properties of three-dimensional plasmonic slot waveguides. Plasmonics: MetallicNanostructures and Their Optical Properties VI. doi:10.1117/12.794322