CST PIC求解器腔体微波粒子束耦合

今天一起看一个PIC求解器案例：

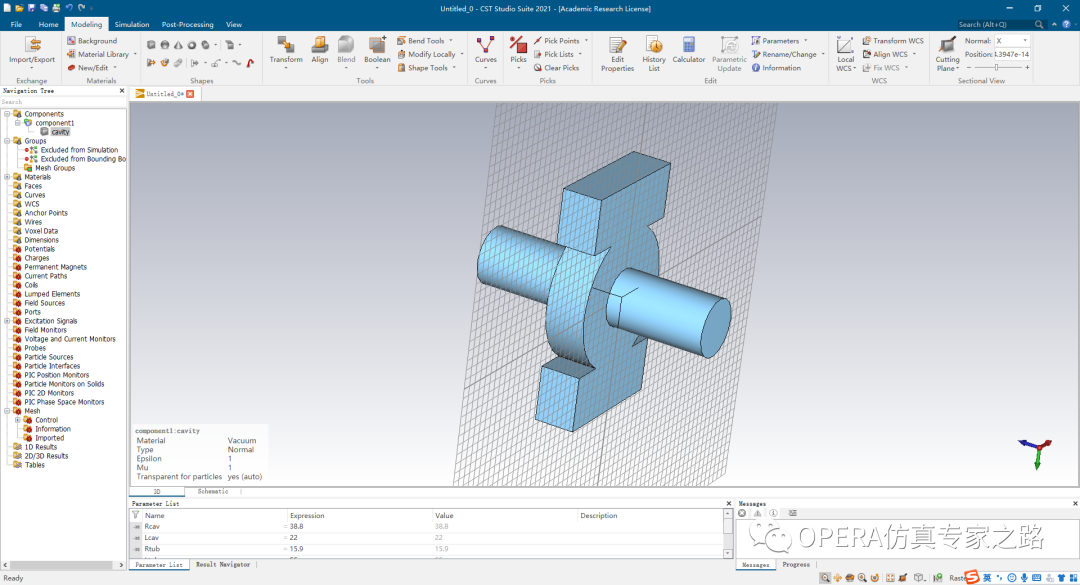
这个呢就是我们今天要整的一个腔体模型。

然后对发射源进行设置，选定发射源边界：

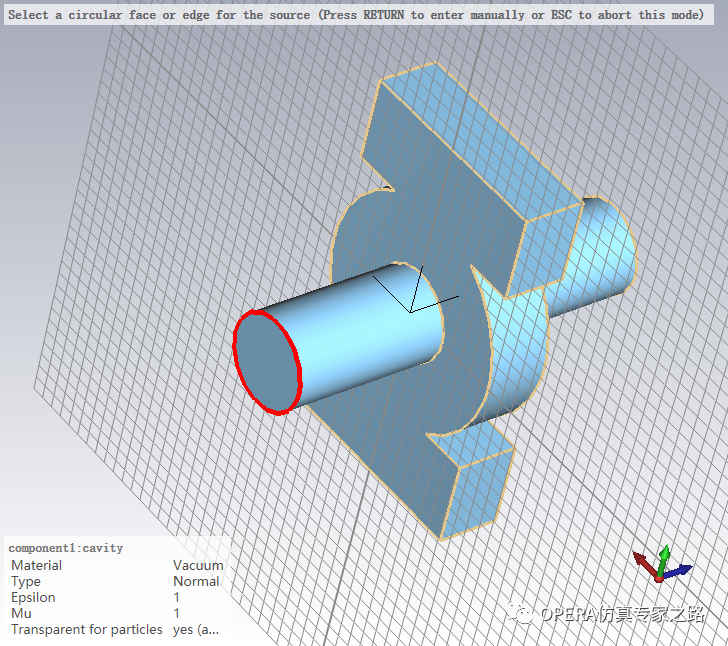
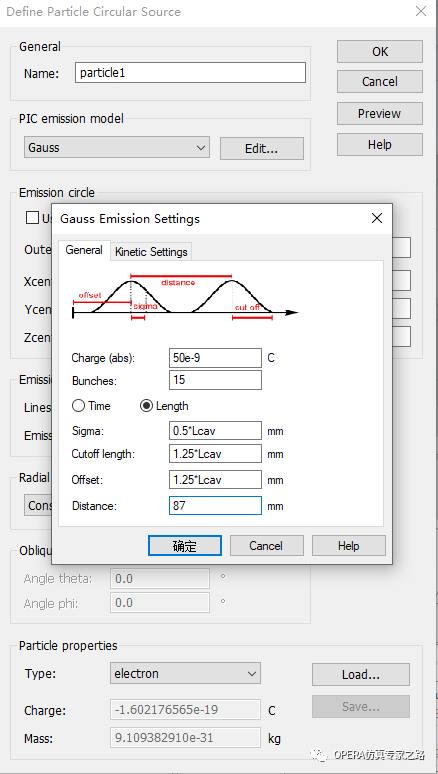
这里对Gaussian高斯发射参数设置给个基本说明：

高斯发射每个脉冲的发射电荷是一个时间相关的高斯函数。菜单里输入指定高斯脉冲的各种参数，如每个脉冲的总电荷、脉冲宽度或两个连续脉冲之间的时间间隔。在没有场的情况下，当粒子具有相同的初始速度时，空间上也满足高斯分布。通过勾选“时间”和“长度”，可以分别在时间和空间维度上定义上述高斯脉冲的参数。

若使用Length空间高斯分布的情况下，发射在时间上仍然是高斯分布的，在kinetic setting动力学设置里会间接或者直接的定义初速度，空间位置参数被转换成等效时间。

在粒子加速器中，一般高斯脉冲参数在空间已知，在空间上即Length定义高斯脉冲的更方便。

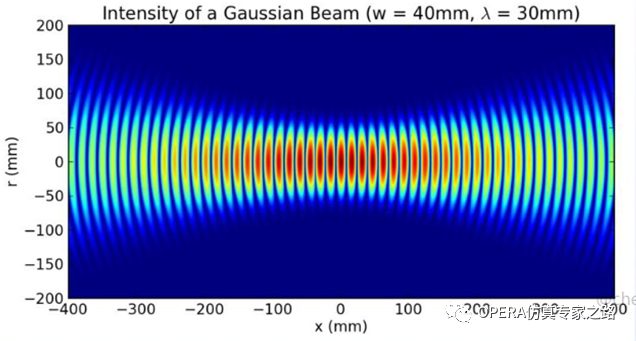
具象点，发射源形式长这样：

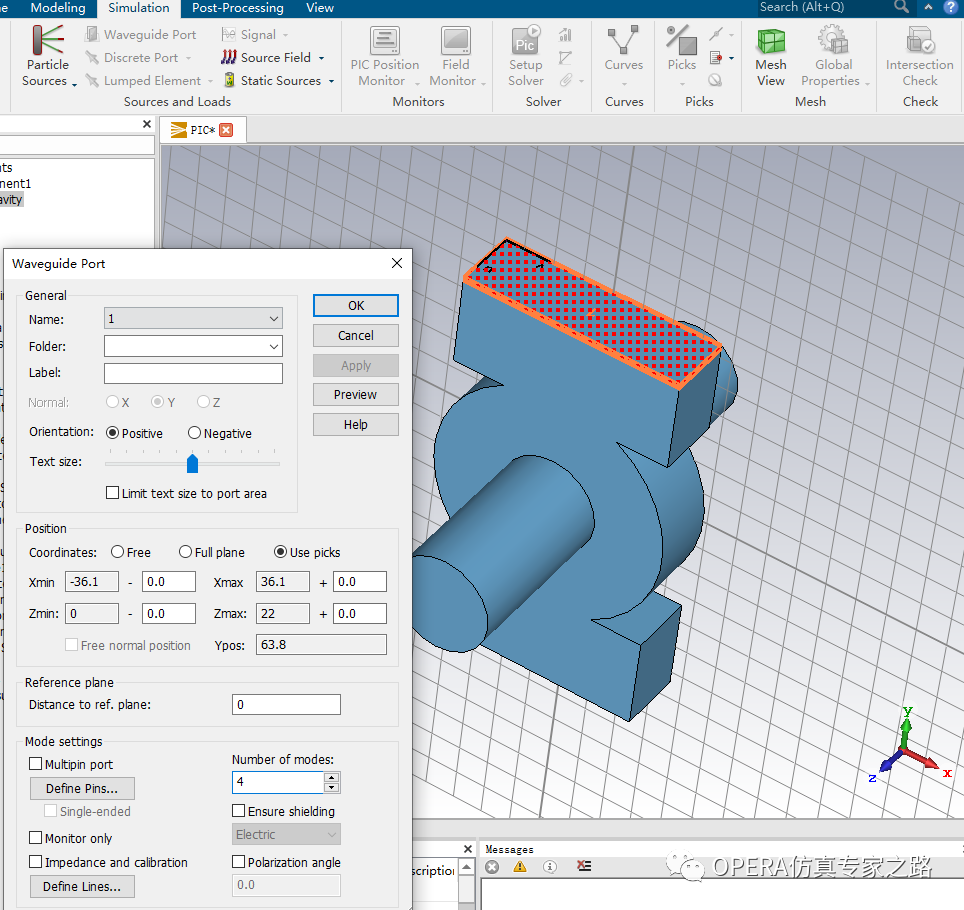
接下来定义微波输入端口：

定义求解频率：

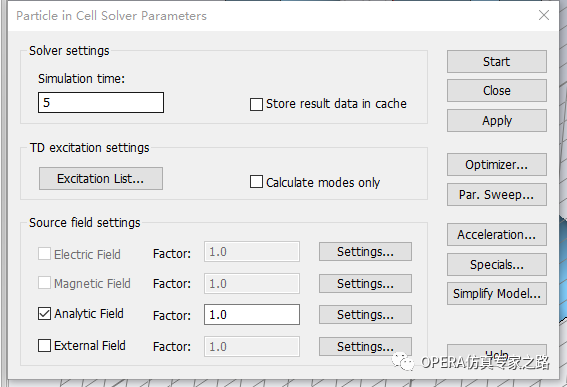
PIC求解器设置：

定义相空间、位置监视器：

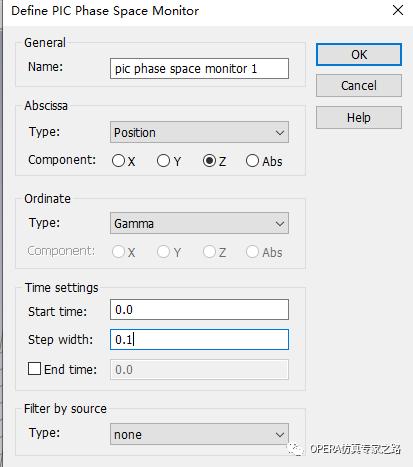
网格使用默认设置就行，然后开始计算，计算完成后查看后处理。

轨迹预览：

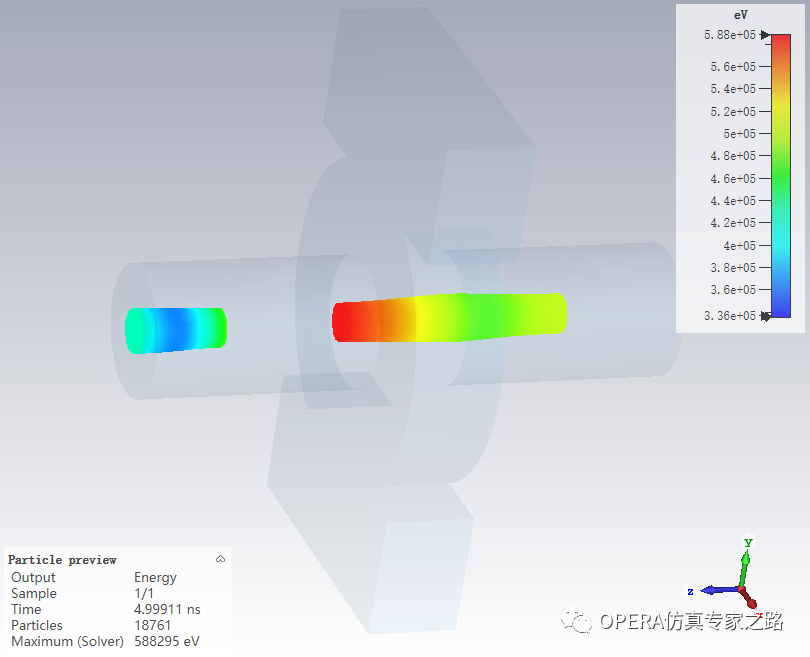
既然是时域，看一下动图，很明显可以看到，发射后的束流经过腔体耦合后形状能量都发生了变化：

然后是洛伦兹因子Gamma的相位图：

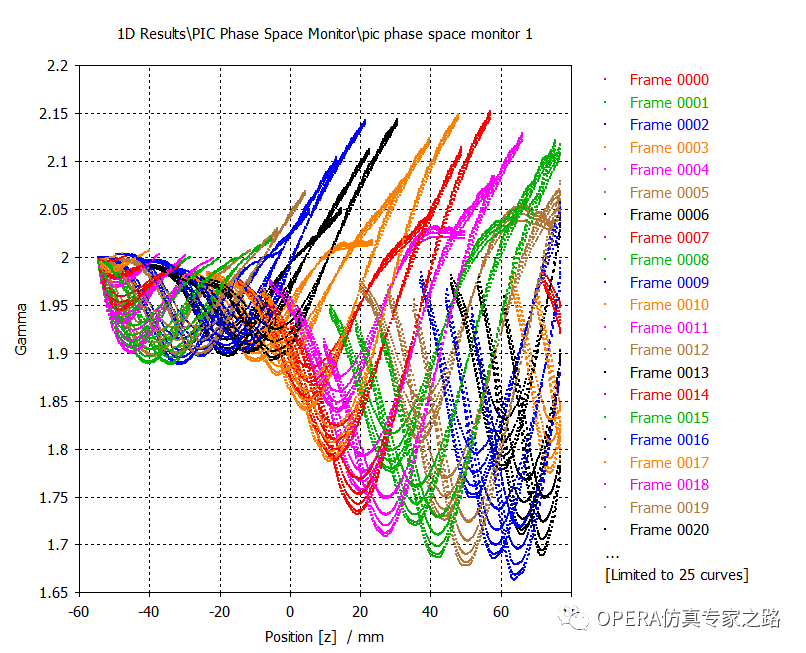
端口1的信号显示粒子束产生了高功率的无线电波：

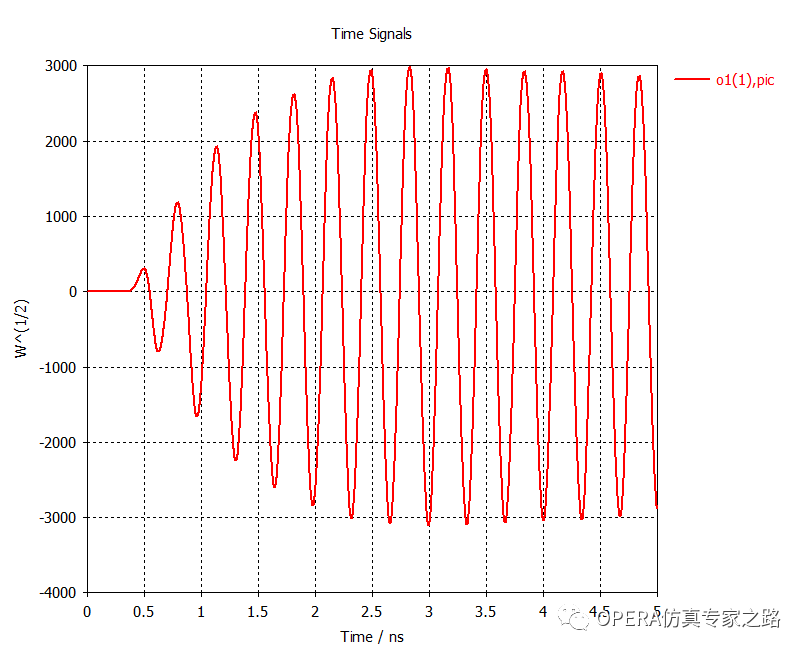
输出信号对应于峰值功率的平方根，计算出输出端从波束提取的平均功率为0.5*3000^2= 4.5 MW。

再看下宏粒子总数与时间的图。当源发出新的粒子时，曲线增大。当粒子撞到东西或被背景吸收时，数量会降低。可以观测二次粒子倍增的情况：

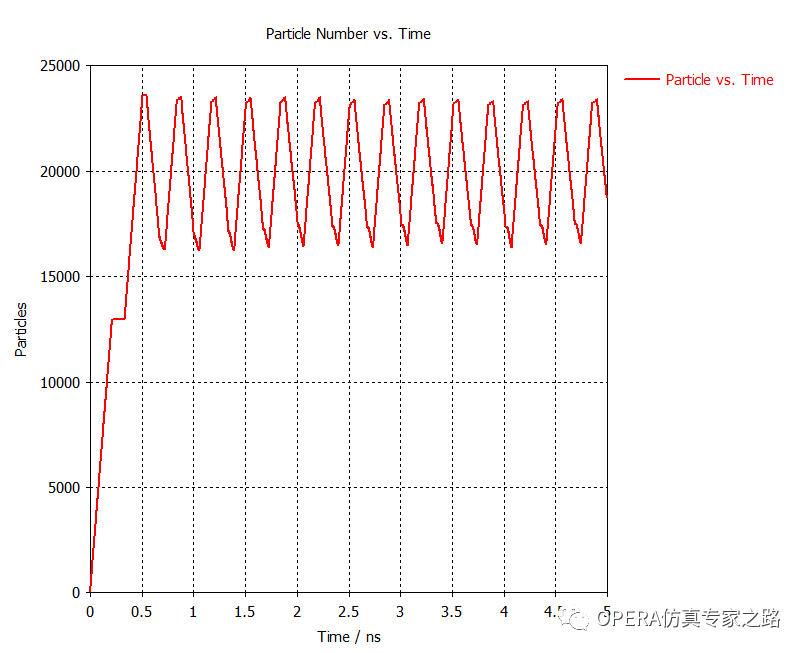
发射电流VS时间图：

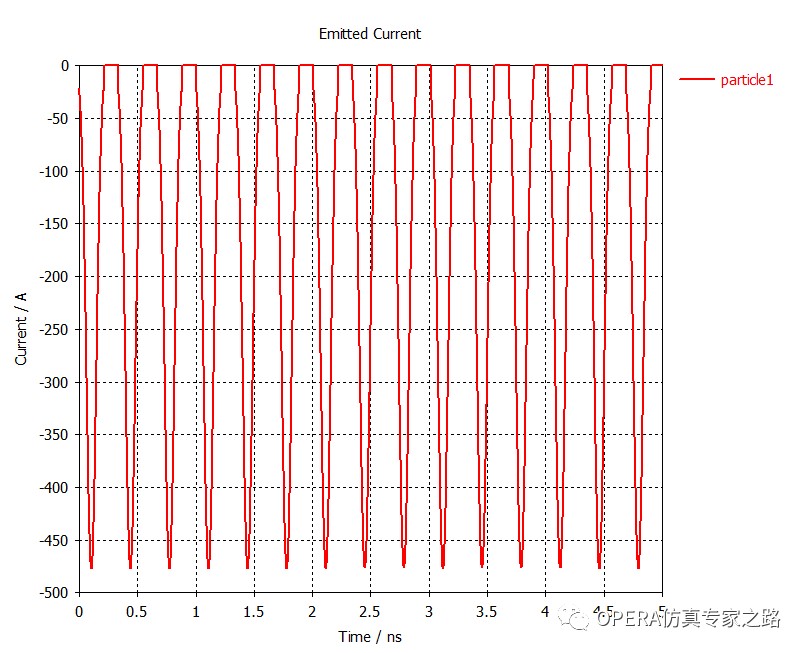
最后来一个电磁波-功率传输图：电磁场从粒子上得到或者损失的功率对应关系。

这就是今天看的案例流水账及一般需要的后处理。