Using a spectral lines task

A spectral lines task ( Home: Simulation New Task... Spectral Lines) can be used to simulate highly nonlinear circuits in frequency domain.

To calculate the spectral lines, a Harmonic Balance (HB) analysis is performed. HB analysis solves for the steady state of a dynamic system and yields the Fourier coefficients of sinusoidal functions for given frequencies. In general, a number of independent excitation frequencies (the tones) are defined for HB analysis. According to the number n of these fundamental frequencies we speak of n-tone analysis. The frequencies considered in the analysis are the mixing frequencies up to a certain number of harmonics specified by the user. The more harmonics are taken into account, the better the results approximate the actual mixing effect.

There are different schemes to evaluate the mixing frequencies. In CST DESIGN STUDIO™ you may choose between the ’Box’ and ’Diamond’ schemes. Independent of the scheme selected, a mixing frequency is calculated from the fundamental frequencies as follows:

Considering n fundamental frequencies f₁, f₂, f₃, &ldots;, f_n with fk< fk₊₁, each associated with a maximum number of harmonics m₁, m₂, m₃, &ldots;, m_n, we obtain the mixing frequencies by

f = | i₁f₁+ i₂f₂+ i₂f₂ + i₃f₂ + &ldots; + i_nf_n |

where | ik_|£ mk

For example, two fundamental frequencies f₁ =100 MHz and f₂ =110 MHz are given. The mixing frequency shown in the image below is addressed by i₁=1, i₂=2. Therefore, it can be calculated from f = 1*f₁ +2*f₂. With f₁ =100 MHz and f₂ =110 MHz we obtain f = 320 MHz.

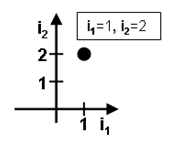
The ’Box’ and ’Diamond’ schemes differ by which frequencies are actually considered in the simulation:

The ’Box’ scheme takes all frequencies into account as specified by the above formula. For n=2, m₁=3 and m₂=2, the mixing frequencies presented in the image below will be considered.

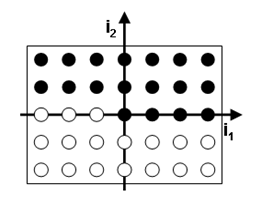
Some of the mixing frequencies are identical to others. For those drawn in white, there is always a counterpart drawn in black. Moreover, some black ones may be identical.

The ’Diamond’ scheme differs from the ’Box’ scheme by the following conditions:

m_l= m_max and

| i₁|+ | i₂ | + | i₃ | + &ldots; + | i_n | £ m_max.

For n=2, m_max=3, for instance, we obtain the mixing frequencies shown in the following image:

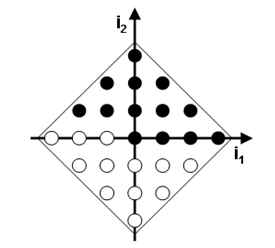
Mixing frequencies drawn in white are always identical to some drawn in black. Some further frequencies may be annotated twice, as mentioned for the "Box" scheme.

Within the Spectral Lines Simulation Task dialog box that you open after selecting the spectral lines task in the Select Simulation Task dialog box, you can specify the fundamental frequencies as well as the evaluation scheme for the mixing frequencies.

The signal sources need to be associated with the fundamental frequencies. Note that only Voltage Signal Sources can be used for Harmonic Balance analysis:

Therefore, let us examine the properties of a Voltage Signal Source inside the Block Properties - Parameters dialog box:

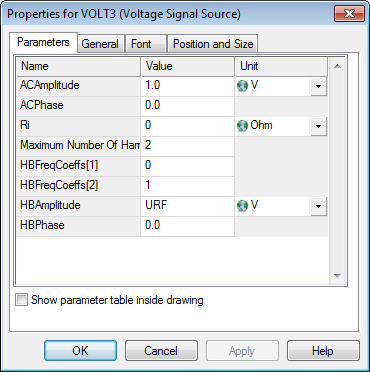
There are four properties that are relevant in the context of Harmonic Balance analysis: ’Maximum Number Of Harmonics’, ’HBFreqCoeffs[k]’ (k=1,2,3,&ldots;), ’HBAmplitude’ and ’HBPhase’. ’HBAmplitude’ and ’HBPhase’ define the amplitude and the phase in degree for the HB excitation signal just like ’ACAmplitude’ and ’ACPhase’ are used for AC simulations.

The values for ’Maximum Number Of Harmonics’ and ’HBFreqCoeffs[k]’ determine the signal frequency. Assign the number of fundamental frequencies n to ’Maximum Number Of Harmonics’. The number of entries ’HBFreqCoeffs[k]’ will change according to the value specified for ’Maximum Number Of Harmonics’. These entries represent coefficients that are used to calculate the signal frequency by

f = HBFreqCoeffs[1]* f₁+HBFreqCoeffs[2]* f₂+&ldots;+HBFreqCoeffs[n]* f_n

with the fundamental frequencies fk specified in the Spectral Lines Simulation Task dialog box. In many cases, you will assign just one of the fundamental frequencies to a signal source. Therefore, set the corresponding ’HBFreqCoeffs[k]’ property to 1 and all others to 0.