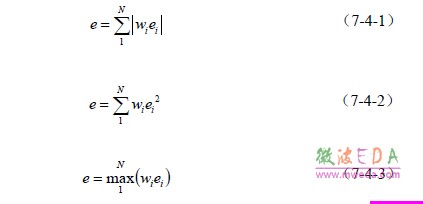7.4 HFSS 优化设计

    优化设计是指 HFSS 软件结合 Optimetrics 模块在一定的约束条件下根据特定的优化算法 对设计的某些参数进行调整，从所有可能的设计变化中寻找出一个满足设计要求的值。优化 设计时，首先需要明确设计要求或设计目标，然后用户根据设计要求创建初始结构模型 （Nominal Design）、定义设计变量并构造目标函数，最后指定优化算法进行优化。HFSS 优化设计的流程如图 7.12 所示。

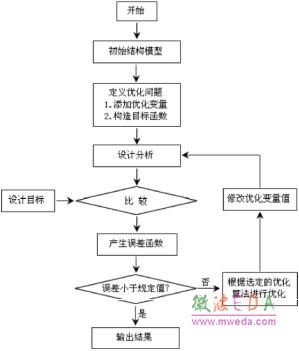
图 7.12 HFSS 优化设计流程

    7.4.1 初始设计

    初始设计或者初始结构模型在 HFSS 中称之为 Nominal Design。用户一般根据理论知识和实际经验给出初始设计，创建初始结构模型。初始设计应该尽量接近真实值，否则会导致优化时间过长，有时甚至得不到全局最优解。

    7.4.2 添加优化变量

    在进行优化设计时，首先需要添加优化变量。如果添加的优化变量是工程变量，需要打开上一节图 7.2 所示的工程变量编辑对话框；如果添加的优化变量是设计变量，需要打开上一节图 7.5 所示的设计变量编辑对话框。然后单击选中该变量编辑对话框中的 Optimization 单选按钮，此时对话框内会列出当前设计中所定义的全部工程变量或者设计变量，可以参考图 7.3，勾选变量对应的 Include 项复选框，把该变量添加为优化变量；同时在Nominal Value、Min 和 Max 项下的文本框分别输入优化变量的初始值、最小值和最大值。在优化设计前，一般先进行参数扫描分析，确定优化变量的初始值和合理的变化区间（即此处的最大值和最小值）。

    7.4.3 构造目标函数

     在优化设计中，为了评价设计结果的好坏以及判断设计是否已经达到要求的目标，必须定义一个判据，软件根据这个判据来决定是否需要继续进行最优搜索，这个判据就称为目标函数。 目标函数需要用户根据具体的设计目标进行构造，例如在第 2 章的设计实例中，设计目标是在10GHz 工作频率处，端口3 的输出功率是端口2 输出功率的两倍，则可以构造目标函数 mag(S(port3，port1))* mag(S(port3，port1))－2* mag(S(port2，port1))* mag(S(port2，port1))=0。 添加了优化变量后，从主菜单栏选择【HFSS】→【Optimetrics Analysis】→【Add Optimization】 命令，或者右键单击工程树下的 Optimetrics 节点，从弹出菜单中选择【Add】→ 【Optimization】 命令，打开如图 7.13 所示的优化设置对话框，目标函数可以在该对话框中定义。

图 7.13 “优化设置”对话框

    对于简单的目标函数，可以在该对话框 Calculation 下的文本框中直接输入构造的目标函数；对于复杂的目标函数，可以先定义输出变量（Output Variables），然后使用定义的输出变量来构造目标函数。例如，在第 2 章中定义了两个输出变量 Power21= mag(S(port2，port1))* mag(S(port2，port1))，Power31= mag(S(port3，port1))* mag(S(port3，port1))，则目标函数相应地可以简化为 Power31－2*Power21=0。

    1．加权函数和规范类型

    在有些设计中，为了达到设计要求，需要设置多个目标函数。另外，目标函数所包含的有些性能指标是互相矛盾或互相制约的，一般很难保证全部指标都达到最优。在这两种情况下，可以给每个目标函数分配一个加权值，加权值越大，表示该目标函数越重要；借助于选用适当的加权函数，可以保证重要指标的设计要求。加权函数值可以在图 7.13 所示的“优化设置”对话框 Weight 项下的文本框中输入。

     图 7.13 所示的对话框中，选中右下角的 Show Advanced Options 复选框，则会在对话框 右上角显示 Cost Function Norm 项。该项用于设置误差计算的规范类型，在其下拉列表中有3 种规范类型可供选择，分别为 L1、L2 和Maximum。这 3 种规范类型定义了3 种计算目标函数误差的方法。

    对于有多个目标函数的问题，误差函数值是所有目标函数误差值的加权和，对于 L1 、L2 和Maximum规范类型，误差函数分别定义为：

    式中，wi和ei分别代表第i 个目标函数的加权值和误差值。

    在定义目标函数时，目标函数可以是等于、大于等于或者小于等于某个目标值；对应的， 在图 7.13 所示对话框的 Condition 处分别选择 = 、>=或者<=。假设分别用si和 gi表示第 i 个目标函数的仿真计算值和真实值，则对于上述3 种情况，第 i 个目标函数误差值ei定义如下。

    优化运算时，当加权后总的误差函数值小于等于设定的优化阈值，优化完成。

    2．优化阈值

    优化阈值是优化过程终止的判别标准，当目标函数的值小于或等于优化阈值时，优化分析完成。图 7.13 所示对话框的左下角 Acceptable 处可以设置优化阈值。优化阈值可以是一个复数。

    3．目标函数的噪声

    使用有限元法分析电磁问题时，网格剖分的变化会给目标函数引入各种噪声。在使用拟 牛顿优化算法和模式搜索优化算法时，需要提供噪声的估算值，以评估求解过程中网格的变化对目标函数的影响。可以在图 7.13 所示对话框的 Noise 处设置目标函数的噪声。

    7.4.4 优化算法

    在 HFSS11 版本中，Optimetrics 模块共支持 5 种优化算法，分别是非线性顺序编程算法 （Sequential Nonlinear Progra mming，SNLP）、混合整数非线性顺序编程算法（Sequential  Mixed-Integer Nonlinear Progra mming，SMINLP）、拟牛顿法（Quasi-Newton）、模式搜索法 （Pattern Search）和遗传算法（Genetic Algorithm）。在图 7.13 所示的“优化设置”对话框中， 单击对话框左上方Optimizer 处的下拉列表，可以选择这 5 种优化算法。多数情况下，推荐 用户选择使用 SNLP 优化算法。 下面分别对这5 种优化算法做个简单的介绍。

    1．拟牛顿法

    牛顿法的基本思想是在极小点附近通过对目标函数 f(x)作二阶泰勒（Taylor）展开，进而找到 f(x)的极小点的估计值。拟牛顿法只有在目标函数的噪声很小的情况下使用是足够准确的，如果目标函数的噪声 在工程是十分显著的，需要使用模式搜索优化算法来得到最优结果。

    2．模式搜索法

    模式搜索法是求解最优化问题的一种直接搜索算法，它不用目标函数与约束函数的导数信息而只用函数值信息，是求解不可导或求导代价较大的最优化问题的一种有效的算法。 该算法由 Hooke 和 Jeeves 于 1961 年提出的，算法的基本思想从几何意义上讲是寻找具有较小函数值的“山谷”，力图使迭代产生的序列沿“山谷”走向逼近极小点。模式搜索法由两种搜索移动方式组成，一是探测移动，一是模式移动，两种搜索移动方式交替进行。探测移动的目的是寻找目标函数的下降方向，模式移动是沿着下降方向的一种加速运动，目的是以较快的速度、较少的搜索次数逼近目标函数在下降方向的极小点。

    模式搜索方法对目标函数的噪声不敏感。

    3．非线性顺序编程算法

    和拟牛顿法相似，非线性顺序编程算法（SNLP）适合解决目标函数的噪声较小的问题，而且SNLP 算法中引入了噪声滤波，可以适当地降低噪声的影响。SNLP 算法采用 RSM（Response Surface Modeling）技术，可以更准确地估计出目标函数值，相对于拟牛顿法，具有更快的收敛 速度。另外，SNLP 算法允许使用非线性约束，这比拟牛顿法和模式搜索法具有更广的使用范围。

    对于多数 HFSS 优化设计问题，推荐用户选择使用 SNLP 算法。

    4．混合整数非线性顺序编程算法

    混合整数非线性顺序编程算法（SMINLP）能够优化具有连续变量和整数变量的问题， 该算法和非线性顺序编程算法相似，不同点是 SMINLP 算法需要标记出整数变量。

    5．遗传算法

    遗传算法是 20 世纪 50 年代初一些生物学家尝试用计算机模拟生物系统演化时提出的。遗传算法是模拟生物通过基因的遗传和变异有效地达到一种稳定的优化状态的繁殖和选择过 程，而建立的一种简单而又有效的搜索算法。遗传算法运用随机而非确定性的规则对一族而非一个点进行全局而非局部地搜索，仅利用目标函数而不要求其导数信息或其他附加限制。 遗传算法虽然在特定问题上也许不是效率最高的，但其效率远高于传统随机算法，是一种普 遍适用于各种问题的有效算法。 遗传算法的主要思路是：用基因代表问题的参数，用染色体（在计算机里为字符串）代 表问题的解，从而得到一个由具有不同染色体的个体组成的群体。这个群体在特定的问题环 境里生存竞争，适者有最好的机会生存和产生后代。后代随机化地继承了父代的最好特征， 并在生存环境的控制支配下继续这一过程。群体的染色体都将逐渐适应环境，不断进化，最 后收敛到一族最适应环境的类似个体，此时即得到问题的最优解。