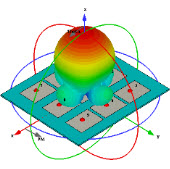
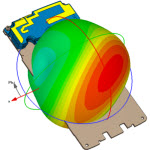
如果物体是匀速的呢?由多普勒频率可以求出时间来么?
是不是匀速好象没什么差别,你的已知量都是一个频移,可以由此求速度,还需要
别的参照,否则天体距离就太好定了。
用天线的话直接可以得出多普勒频率么?还是要由速度来求?
Next: Dynamic Retrieval Up: Dynamic Retrievals and Related Previous: Introduction
Doppler Radar Analysis
This chapter focuses on retrieval techniques that generally employ Doppler radar data. Scanning Doppler radars are an extremely powerful tool for studying atmospheric circulations with the ability to provide about 104 measurements of the wind field per second at relatively high spatial resolutions with areas of the order of 1011 m2 sampled in time scales of well less than a minute. The relative utility of these radars is evidenced by their widespread usage within the research community beginning in the late 1960s and early 1970s and their subsequent adoption by operational weather centers in many countries throughout the world. In this section we will only provide a brief overview of those aspects of Doppler radar analysis that are necessary to better understand the retrieval concept.
To begin we note that Doppler radars measure only the radial component of the wind, while the quantities of general meteorological interest and the inputs needed for the retrieval technique are the three Cartesian components of the wind field. The relationship between the radial wind, Vr and the horizontal (u, v) and vertical (w) components of the wind can be related as
(13.2)
with (W) defined as (w + wp ) (where wp is the particle fallspeed) and the radar range Ri is defined as
Ri = [(x - xi)2 + (y - yi)2 + (z-zi)2)]1/2. (13.3)
From these relationships it is clearly evident that deriving the Cartesian components of the wind field from Doppler radar measurements requires more than one Doppler radar and/or a number of assumptions. In practice there are a wide variety of techniques available (i.e., Ray 1990 for a review) depending upon the number of radars, the geometry of the radar array and the meteorological phenomena of interest.
While realizing that there are a variety of options available we will highlight some commonly used approaches to derive the Cartesian components of the wind field. As noted by Armijo (1969) perhaps the most straight forward solution to the problem is to have three independent radar observations and to directly solve a matrix of equations for (u, v, W). Subsequently the vertical air motion, (w), can be obtained through estimating the particle fall speed (wp) from radar measurements of reflectivity and subtracted this estimate from the values of (W) obtained from solving the matrix.
Of course in order to solve the matrix the first step is generally to interpolate the measurements of radial velocity from each radar onto a common Cartesian grid. The interpolation concepts described in the previous chapter come into play in this step of the analysis with, for example, the Cressman filter or variations of linear interpolation common choices among researchers. From relationship between the radial velocity and the Cartesian components it is evident that any uncertainty in the measurement of radial velocity will result in an error in the Cartesian winds with a strong geometric dependence. For example, a horizontal cross-section of the errors in the horizontal wind components given a 1 m s-1 error in the measured radial component are shown in Fig. 13.1:
--------------------------------------------------------------------------------
Figure 13.1: Error in the horizontal wind estimates obtained from applying a 1 m s-1error in the radial velocity field into the solution for the triple Doppler solution of equation (2) from Armijo (1969).
--------------------------------------------------------------------------------
The estimates of vertical component, (W), are particularly sensitive to measurement errors at low elevation angles (i.e. when z - zi is small). In practice this constraint results in large errors in (W) at elevation angles less than approximately 45 degrees. For this reason, the vertical velocity (w) is more typically estimated from integration of the anelastic mass continuity equation (Ogura and Phillips, 1962) in the form
(13.4)
.
Here is some "basic" atmospheric density which could be taken to be the area averaged density or other representative density obtained, e.g., from an atmospheric sounding. Ogura and Phillips originally considered only the basic density corresponding to an atmosphere in hydrostatic and adiabatic balance, but in later work (e.g.,Durran 198???) the initial concept has been shown to be applicable to arbitrary representative density provided that the deviation from the ``basic" density is small. As was discussed by Gal-Chen and Wyngaard (1984) and others such vertical integration of the divergence to obtain the vertical motions is fraught with danger, because of the need to calculate derivatives from noisy measurements, the inherent smoothing associated with Doppler radar measurements and the vertical integration which amplifies features with small horizontal wave lengths and long vertical wave lengths. Nevertheless, techniques that reduce such errors are available (Ray 1980; Gal-Chen,1982; Chong and Testud, 1983; Ziegler et al. 1983; Gal-Chen and Xu, 1994).
An implication of invoking the continuity equation to derive the vertical motions is that the necessity for a third radar to solve the systems of equations can be relaxed. In Cartesian coordinates, the solution to the two radar system is iterative, updating (W) to obtain (u,v) (Brandes 1978). This dual-Doppler approach can also be extended to more than two radars (Ray and Sangren 1983). An alternative to the two radar solution in Cartesian coordinates is to employ a special subset of cylindrical coordinates so that a a direct solution is possible. The pioneering work by Ray et al. (1975), Miller (1975), and Kropfli and Miller (1975, 1976) used the approach of employing cylindrical coordinates. Although the direct solution is appealing, in this approach the solutions are typically interpolated to a Cartesian grid for subsequent analysis and for graphical display.
In the use of the continuity equation and the interpolation of the data from the different radars to a common grid, an important issue that arises is the treatment of time. In the relationships given thus far it is implicitly assumed that all the measurements are taken simultaneously. In practice, there is a finite time necessary for each radar to scan the analysis domain. The importance of time differences between observations might at first seem relatively unimportant in this application given that a Doppler radar scan is relatively rapid, typically taking only 2-8 minutes to complete. In contrast for example, many of the applications of the data assimilation methods described in the previous chapter can successfully ignore far larger time differences such as the 1 h time period that it takes to complete a radiosonde measurement. The relative importance of the treatment of time differences in the radar analysis is directly dependent on the time scale at which the meteorological feature evolves and/or the speed at which it advects across the analysis grid relative to the scanning time. For example, if the evolution of the system is rapid enough so that significant evolution occurs during the scanning time (as can easily happen with convection) then errors can arise "locally" at a grid point due to time differences among the different radars' observations of radial velocity at that grid point. The impact of errors induced by time differences between the individual radars at a point may be reduced somewhat through careful coordination of the scans between the radars. However, a "global" error can also arise from evolution when the continuity equation is invoked to link vertical layers that were scanned at different times. The time differences between the top and bottom of the scan can be very large, since most radar scanning strategies involve scanning in the azimuthal plane at many different elevation angles starting at the bottom (or top) of a storm. Unfortunately, this error is more difficult to detect and reduce without either more rapidly scanning radars and/or resorting to more sophisticated analysis techniques that treat time as an additional variable.
As previously mentioned, temporal errors can also result even in the absence of evolution if the advection is rapid. In this situation the global error from linking of different vertical layers by the continuity equation can be large resulting in even larger qualitative errors in the derivation of vertical motions. For example consider a vertically oriented updraft with convergence in the lower layers and divergence aloft (Fig. 13.2). The presence of strong advection will displace the convergence and divergence couplets in space which in the worst case scenario will create an updraft and downdraft couplet in place of a single updraft. Fortunately the advection errors are easier to treat through deriving an optimal frame of reference from the observations and placing the data in this optimal frame of reference while retaining the geometry of the initial measurement in the solution technique (e.g., Gal-Chen 1982; Chong and Roux 1983).
--------------------------------------------------------------------------------
Figure 13.2: Schematic of the temporal error that can result solely due to the advection of a steady state wind field across a radar volume.
--------------------------------------------------------------------------------
We have only provided a brief overview of the broad area of Doppler analysis to provide some necessary background for the discussion of the retrieval techniques that follow. The interested reader is referred to Atlas (1990) or other texts for further information concerning the historical development of this instrument, some background on measurement techniques and the wide variety of research applications. For example, the chapter by Ray (1990) within the Atlas text provides an excellent discussion of many of the issues discussed in this section. In addition to these historical treatments the reader is referred to recent work within the Doppler analysis field such as state-of-the-art analysis techniques dealing with scanning, multiple beam, air-borne systems that have special analysis requirements (e.g., Kabeche and Testud, 1995; Chong and Testud 1996; Jorgensen et al. 1996; Bousquet and Chong 1997). Before undertaking the development of a Doppler radar analysis system, the potential researcher should also be aware that some large meteorological research centers routinely make available to interested researchers detailed software packages to derive Cartesian wind fields from radial velocity measurements such as the CEDRIC code developed at the National Center for Atmospheric Research (Mohr et al. 1986) or the ODDAN software developed at the National Severe Storms Laboratory (Kessinger et al. 1987).
--------------------------------------------------------------------------------
Next: Dynamic Retrieval Up: Dynamic Retrievals and Related Previous: Introduction
--------------------------------------------------------------------------------
NCAR Advanced Study Program
http://www.asp.ucar.edu
相关文章:
- 求助:请问用HFSS可以在多高的频率下计算?(05-08)
- 晶体管的频率!(05-08)
- 请问信号发射接收之后有个“偏移频率”,到底原因是什么呢?请(05-08)
- 无线频率资源划分(05-08)
- hfss仿真矩形微带天线,谐振频率怎么看?(05-08)
- hfss Eigenmode计算出来的频率的问题~~~~~~~~~~~!(05-08)