请教耦合矩阵中E（s）的求法？

05-08

我按照1999年camera的文章的方法，算出的耦合矩阵不对，不知道为什么，想请教一下！
具体参数f0=887mhz，bw=4mhz，rl<= 22db,传输零点为在+1.5j和-1.5j两处，算出的
f（s）=8.0926*s^4 +6.4258*s^2 +0.4444;
p(s)=2-0.8888s^2;
e（s）是先求出极点，然后得出的其多项式，如下：
e(s)=8.0926*s^4+33.4856s^3+62.8538s^2+63.0843s+47.6908;
不知道这样做可以不可以?
通过这样算出的T1k*Tnk和Tnk^2虽然是实数，但不是正实数，肯定不对！请教大牛们，能不能解答一下，怎么算e（s）呢?
谢谢

貌似搞这个的人很多
好窄的带宽……
Foled型矩阵=
0 0.0047 -0.0000 -0.0000 -0.0000 0.0000 0
0.0047 -0.0000 0.0040 0.0000 0.0000 0.0000 0.0000
-0.0000 0.0040 0.0000 0.0027 -0.0000 -0.0011 0.0000
-0.0000 0.0000 0.0027 0.0000 0.0035 -0.0000 0.0000
-0.0000 0.0000 -0.0000 0.0035 0.0000 0.0038 -0.0000
0.0000 0.0000 -0.0011 -0.0000 0.0038 0.0000 0.0047
0 0.0000 0.0000 0.0000 -0.0000 0.0047 0
Cul de Sac型矩阵 =
0 0.0047 -0.0000 -0.0000 -0.0000 0.0000 0
0.0047 -0.0000 0.0032 0.0000 0.0024 0.0000 0.0000
-0.0000 0.0032 0.0000 -0.0000 -0.0000 -0.0032 0.0000
-0.0000 0.0000 0 0.0000 0.0044 -0.0000 0.0000
-0.0000 0.0024 0.0000 0.0044 -0.0000 0.0024 -0.0000
0.0000 0.0000 -0.0032 -0.0000 0.0024 0.0000 0.0047
0 0.0000 0.0000 0.0000 -0.0000 0.0047 0

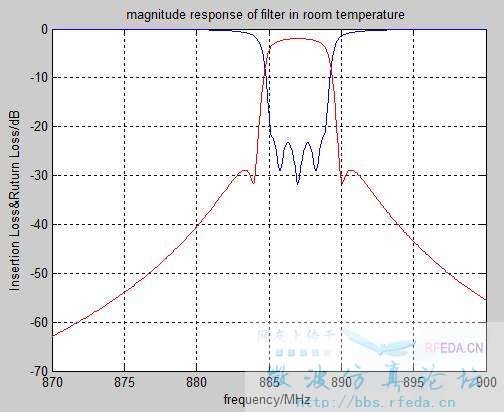
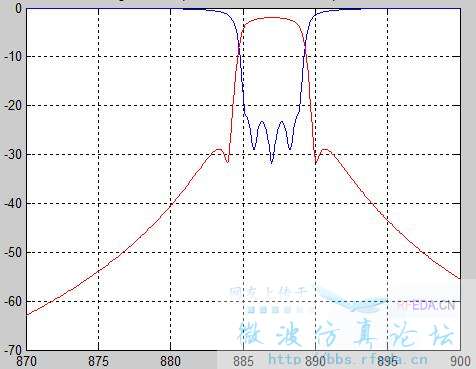
你这个带一个交叉耦合哦
是三腔的么?
如果是的话，方法应该没错

这个很好求呀，用|S11|^2+|S21|^2=1这个条件，把上述多项式带入。然后求根，取左半平面的根组合一下就可以得到e（s）了。

我用的是Cul de Sac型。有疑问：我设计的是4阶的微带滤波器，具体形式参照DR hongjiasheng的形式，即四个方形的微带谐振器。我得出的是6阶矩阵，为什么您得出的是7阶?
能否详细说明一下?
太感谢了！

先求出纹波系数a，根据e*e=f*f+p*p/a/a，得到e*e的多项式，求出e*e的根，选择s域中下半平面的根作为E（s）的根，反求出E（s）就可以了。注意在求解过程中,f,p ,e 的最高次项系数必须为1，而且要同时在s域求解。

上一篇：求关于射频耦合器的国内外发展动态的文章
下一篇：在做关于耦合器的毕业设计，问个问题

射频专业培训教程推荐