问个电磁场边界条件的问题

12-13

1. 磁场强度H仅与产生该磁场的电流有关, 与介质的磁导率无关(毕奥沙伐定律)
2. 磁通密度B=μH(磁通密度的定义)
3. 磁通密度B是连续闭合的矢量场(麦克斯韦方程组第三个方程)
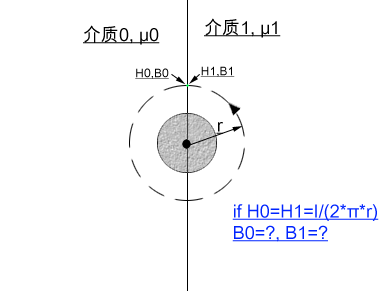
那么如果两种介质的分界面上有一根导体有电流I, 该怎么理解两种分界面处的磁场强度和磁通密度呢? (见附件, 电流方向垂直于屏幕)
根据1, 则分界面上的磁场强度相等, H0=H1
根据3, 分界面上的磁通密度相等, B0=B1
那么势必要求μ0=μ1, 矛盾了!
请问问题出在哪里呢? 谢谢!

问题出在你概念错误。麦克斯韦第三方程是B的散度为0，而不是B的旋度为0。在两个媒质的交界面上做个封闭的曲面，而不是曲线，就会发现，穿过该曲面的磁通量等于0。在分解面上，B的切向分量不一定连续，而法向分量必然连续，而在本题中，法向分量都等于0，而切向分量不相同。你错误的将不相等的切向分量当成法向分量了。

你说的是对的, 但我也没有理解错, 麦克斯韦方程组第三个公式是磁通量散度为0, 也就意味着磁通量是闭合连续的矢量场, 因为闭合连续的矢量场中任何一点的散度都为0.
我给的图里, 分界面是与屏幕垂直的, 电流线也与屏幕垂直, 正好在分界面上, 那么根据右手法则, 上面一点的场强和磁通都是从右向左垂直与分界面的, 也就是说切向分量为0, 法向分量不为0. 而不是像你说的那样法向方向为0.
根据毕奥沙伐定理(其实是麦克斯韦方程组第一个公式在仅考虑静电场的时候), H的分布仅与电流有关, 与介质无关, 也就是电流的空间分布就唯一的确定了H的场分布, 换句话说, 无论介质的分界面在哪里, 什么形状, H场的空间分布仅唯一的被电流的空间位置所决定, 不是吗? 那就应该有H在分界面上无论是切向还是法向都是连续的, 而不应该是书里说的仅切向方向连续. 我所不理解的矛盾就在这里. 能否再谈谈你的看法?

那界面上并不是空空荡荡的啊，既然u存在，必然存在对应的磁核分布来保证B法向连续

连续只能保证法向连续

如果是这样，问题就出在你计算H的公式上，也就是H=I/（2*PI*R），这个公式成立的条件是空间中物质和边界的分布是旋转对称的，也就是说，在任意的phi角度上，物质分布和边界分布都是一样，因而有H与phi角度无关，所以才有integrate(H*dl)=2*pi*R*H=I。而在你这个问题中，由于两个媒质各占一半的空间，打破了旋转对称性，上述公式必然不成立，所以没有H=I/（2*PI*R）。也就是说，在两个媒质中，H是不一样的

上一篇：求教：差分电路的阻抗匹配，望指点
下一篇：请推荐个WCDMA频段1dB压缩点30W的管子吧，无奈了

射频专业培训教程推荐