球形分布的期望和方差怎么计算？

对一个误差函数进行分析，每一次的采样值取得的点都位于一个球内，那么这个点服从的分布是叫球形分布吧，球的中心和半径都是已知的，我想这道这样的分布的期望和方差怎么计算？

若果球心在原点，半径是2的话，那么期望是0，方差是4吗？

由球体的对称性，期望为0，半径R=2时，方差是2.4
均匀球体分布matlab代码
function [x,y,z] = rand_pick_sphere(n,a,b,X,Y,Z)
% Uniform points in a shell of inner radius a, outer radius b and center at
% (X,Y,Z)
% [x,y,z] = rand_pick_sphere(300,.5,.6);  % 300 points in shell between
% r = .5 and r = .6, with center at origin.
if nargin==3
   X = 0;
   Y = 0;
   Z = 0;
end
r1 = (rand(n,1)*(b^3-a^3)+a^3).^(1/3);
phi1 = acos(-1 + 2*rand(n,1));
th1 = 2*pi*rand(n,1);
% Convert to cart.
x = r1sin(phi1)sin(th1) + X;
y = r1sin(phi1)cos(th1) + Y;
z = r1cos(phi1) + Z;
matlab验证一下
[x,y,z]=rand_pick_sphere(100000,0,2);
mean(x)
mean(y)
mean(z)
mean(x.^2+y.^2+z.^2)

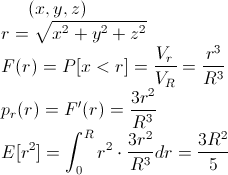
哈哈，非常感谢你的回答。

不对