对于仿真软件相位方向图计算的讨论
05-08
摘 要:GPS 接收天线,反射面馈源等天线的设计需要对于天线的相位特征加以考虑。仿真软件在相位方向图的计算上可能存在一定误差,继而影响到对于相位特征有较高要求的天线设计。本篇文章通过比较对于同一模型在不同仿真仿真软件下与不同求解设臵下的计算结果,说明仿真软件在天线相位方向图上的误差,并主要分析该误差在CST 微波工作室下产生的原因。1 引言由于高精度的全球定位系统需要用户段的接收天线能够准确地测量载波相位,因此指标要求天线在近上半空间(俯仰角在±80°范围内)的相位误差小于10°,在L1 频段(1.575GHz)该指标对应长度为5mm[1]。在一些文献中,对于仿真模型的辐射场相位误差描述则达到了0.1mm 甚至0.01mm 数量级。然而仿真软件的相位方向图计算能否达到这一精度则少有文章提及。本篇文章首先通过二元点源阵与半波阵子天线理论模型,说明计算边界大小对于相位方向图的影响,继而分别在CST 微波工作室,HFSS 与FekoSuite 电磁仿真软件中建立半波振子天线模型,并将仿真的相位方向图结果与理论计算值进行比较。最后则分析CST 微波工作室相位方向图计算误差产生的原因。2 计算边界对于二元点源阵相位方向图的影响IEEE 对于天线相位方向图与相位中心定义如下[2]:相位方向图为天线辐射场矢量的相位空间分布,而相位中心则是与天线相关的一个点,在以该点为球心半径延伸至远区场的球面整体或是球面的一部分上,天线辐射场的相位几乎是不变的。著作[3]中以如图1 所示的等幅同相的二元理想各向同性点源阵为例,说明相位方向图的结果与计算坐标系原点选取的关系,并指出当计算辐射场的坐标系原点选取在二元阵的中点时,二元阵的相位方向图为阶跃函数:若阵元间距d 小于二分之波长,那么二元阵的相位方向图函数为一常数,。当天线阵元间距大于二分之波长时,天线幅度方向图会有零点产生,在幅度方向图零点位置相位方向图会出现180°跳变。
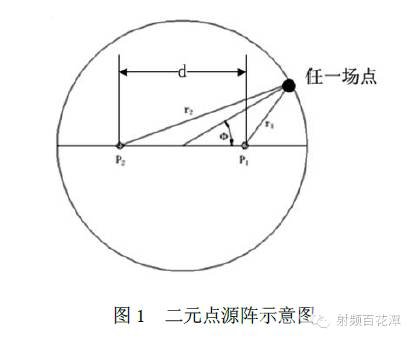
 可见在有限大的计算边界下,二元阵的相位方向图会因为计算边界大小而变化。当计算边界越大时,相位方向图的波动越小,其函数表达式约接近于无限大边界下的阶跃函数。
可见在有限大的计算边界下,二元阵的相位方向图会因为计算边界大小而变化。当计算边界越大时,相位方向图的波动越小,其函数表达式约接近于无限大边界下的阶跃函数。
 3 理论与仿真计算半波阵子E 面相位方向图比较继而分析有限长度线源的相位方向图。令长度为d 的线源沿z 轴放置,坐标原点位于线源几何中心。那么在球坐标系下任一场点(X,Y,Z)距离线源上任一点(0,0,z)距离r1 可写作
3 理论与仿真计算半波阵子E 面相位方向图比较继而分析有限长度线源的相位方向图。令长度为d 的线源沿z 轴放置,坐标原点位于线源几何中心。那么在球坐标系下任一场点(X,Y,Z)距离线源上任一点(0,0,z)距离r1 可写作
 那么由公式即可绘出半波阵子天线在不同计算半径r 下的E 面的相位方向图并与通过CST Microwave Studio, Feko Suite 与HFSS 三种仿真软件计算的相位方向图进行比较。仿真软件中的振子天线工作在L1 频段(1.575GHz)附近,振子臂半径为1mm,臂长经调节为41mm( 0.21入)。比较的结果如图4 所示。
那么由公式即可绘出半波阵子天线在不同计算半径r 下的E 面的相位方向图并与通过CST Microwave Studio, Feko Suite 与HFSS 三种仿真软件计算的相位方向图进行比较。仿真软件中的振子天线工作在L1 频段(1.575GHz)附近,振子臂半径为1mm,臂长经调节为41mm( 0.21入)。比较的结果如图4 所示。
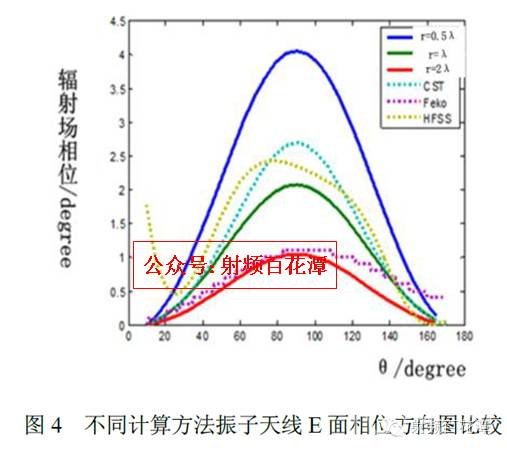 可见于第二节中点源阵相位方向图随半径r 的变化趋势类似,线源天线理论计算的相位方向图波动也随着半径增大而减小。而由于理想的辐射边界应在形状上近似球面且在尺寸上尽量大,由图3 中可见,CST 软件计算得的相位方向图与理论计算在函数曲线上更为相似,这也印证了文章[3]的观点,即CST 的计算边界更近似于球面。通过CST,Feko与HFSS 软件计算得的相位方向图均方根误差分别为0.92°,0.31°与0.82°,在L1 频段分别对应长度为0.48mm,0.16mm 与0.43mm。由于在理想的无穷远边界下,半波阵子天线的E 面相位误差应趋于0。因此对于仿真软件计算得的E 面均方根误差可以认为是仿真软件造成的计算方向图的误差。因此将在下节中讨论如何减小这种仿真软件在相位方向图计算上的误差。4 仿真软件相位方向图计算误差产生分析在HFSS 软件中的辐射边界是用来模拟电磁波朝无穷远辐射的开放问题,而这类问题在天线设计中十分常见。一般使用的辐射边界采用第一阶吸收边界条件(ABC)[4]。文献[5]中的相应章节有对于该类边界条件的讨论,并给出该类吸收边界对于不同极化方式,不同入射角的电磁波的反射系数。而在CST 中计算辐射场则是使用的开放(openadd space)边界条件,[6]中说明该边界条件可以视作PML 边界加上了一些额外的空间用来计算远区场,并提到PML 层数为为取默认的四层就已足够。在[7]中则说明增加PML 层数可以使得局部和总体误差都单调地减小,但是PML 层数过多又会导致计算量的剧增。因此折衷考虑吸收边界效果与计算量,可以选取层数4 至8 层。因此通过调节CST 微波工作室仿真环境下半波阵子天线包括求解频率,计算边界大小(默认为计算频段中频波长的八分之一),PML 边界层数(默认为4 层)的计算设置,来比较天线E 面相位方向图在θ为10°~170°范围内的均方根误差,通过均方根误差值来比较不同设置下相位方向图的计算结果,并将均方根误差值对应到L1 频段波长。比较结果在表1 中给出。仿真采用时域求解器,在不同频率下计算的网格数单元数均为56400 个。
可见于第二节中点源阵相位方向图随半径r 的变化趋势类似,线源天线理论计算的相位方向图波动也随着半径增大而减小。而由于理想的辐射边界应在形状上近似球面且在尺寸上尽量大,由图3 中可见,CST 软件计算得的相位方向图与理论计算在函数曲线上更为相似,这也印证了文章[3]的观点,即CST 的计算边界更近似于球面。通过CST,Feko与HFSS 软件计算得的相位方向图均方根误差分别为0.92°,0.31°与0.82°,在L1 频段分别对应长度为0.48mm,0.16mm 与0.43mm。由于在理想的无穷远边界下,半波阵子天线的E 面相位误差应趋于0。因此对于仿真软件计算得的E 面均方根误差可以认为是仿真软件造成的计算方向图的误差。因此将在下节中讨论如何减小这种仿真软件在相位方向图计算上的误差。4 仿真软件相位方向图计算误差产生分析在HFSS 软件中的辐射边界是用来模拟电磁波朝无穷远辐射的开放问题,而这类问题在天线设计中十分常见。一般使用的辐射边界采用第一阶吸收边界条件(ABC)[4]。文献[5]中的相应章节有对于该类边界条件的讨论,并给出该类吸收边界对于不同极化方式,不同入射角的电磁波的反射系数。而在CST 中计算辐射场则是使用的开放(openadd space)边界条件,[6]中说明该边界条件可以视作PML 边界加上了一些额外的空间用来计算远区场,并提到PML 层数为为取默认的四层就已足够。在[7]中则说明增加PML 层数可以使得局部和总体误差都单调地减小,但是PML 层数过多又会导致计算量的剧增。因此折衷考虑吸收边界效果与计算量,可以选取层数4 至8 层。因此通过调节CST 微波工作室仿真环境下半波阵子天线包括求解频率,计算边界大小(默认为计算频段中频波长的八分之一),PML 边界层数(默认为4 层)的计算设置,来比较天线E 面相位方向图在θ为10°~170°范围内的均方根误差,通过均方根误差值来比较不同设置下相位方向图的计算结果,并将均方根误差值对应到L1 频段波长。比较结果在表1 中给出。仿真采用时域求解器,在不同频率下计算的网格数单元数均为56400 个。
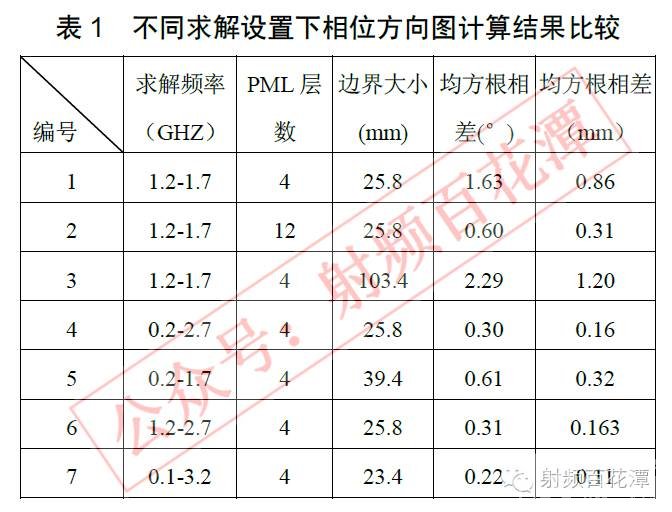 可见,在CST 微波工作室仿真环境下,计算边界大小对于相位方向图计算结果并没有直接影响。增加PML 层数可以在一定范围内减小相位方向图的计算误差。同时相位方向图的计算结果与求解频率关系密切,扩展求解频率范围可以减小相位方向图的均方根误差,即令计算边界更接近于理想的辐射边界。同一天线模型在不同的求解频率下的均方根相差对应到距离可以达到0.75mm(编号1 与编号7 的数据)。经过仿真还发现增加网格单元数,对于相位方向图结果影响不大。5 结论不同仿真软件对于工作在L1 频段的半波振子天线相位方向图均方根误差的结果差值可以达到0.3mm。而在CST 微波工作室下的同一半波阵子天线模型,在不同的求解设置下对于相位方向图的均方根误差计算结果,相差可以达到0.75mm。可见不同仿真软件与同一软件的不同设置对于相位方向图的计算存在一定影响。在CST 微波工作室下扩展求解频率可以在一定程度上减小计算相位方向图的误差。而对于工作在L 波段的卫星接收天线而言,相位方向图均方根误差0.01mm 的精度可能已经超过了仿真软件对于相位方向图计算的误差限。参考文献[1] Tranquilla J M, Colpitts B G. ―GPS antenna design characteristics for high-precision applications‖[J]. Journal of Surveying Engineering, 1989, 115(1): 2-14.[2] IEEE Standard Definitions of Terms for Antennas Sponsored by Antenna Standards Committee of the IEEE Antennas and Propagation Society[3] John D. Kraus, ―Antennas‖ New York : McGraw-Hill, c1988. 2nd ed..pp 137-140[4] Investigation of antenna phase pattern by the electromagnetic simulation software, Ze Shen, Zhenxin Cao,2014 ICCP&HSIC[5] HFSS Help-Assigning boundaries-Assigning Radiation Boundaries;[6] 金建铭(著) 王建国(译), 电磁场有限元方法, 西安电子科技大学出版社,1998,P308~P317。[7] CST Help Content-Boundary Conditions[8] 王秉中, 计算电磁学. 科学出版社, 2002,第四章
可见,在CST 微波工作室仿真环境下,计算边界大小对于相位方向图计算结果并没有直接影响。增加PML 层数可以在一定范围内减小相位方向图的计算误差。同时相位方向图的计算结果与求解频率关系密切,扩展求解频率范围可以减小相位方向图的均方根误差,即令计算边界更接近于理想的辐射边界。同一天线模型在不同的求解频率下的均方根相差对应到距离可以达到0.75mm(编号1 与编号7 的数据)。经过仿真还发现增加网格单元数,对于相位方向图结果影响不大。5 结论不同仿真软件对于工作在L1 频段的半波振子天线相位方向图均方根误差的结果差值可以达到0.3mm。而在CST 微波工作室下的同一半波阵子天线模型,在不同的求解设置下对于相位方向图的均方根误差计算结果,相差可以达到0.75mm。可见不同仿真软件与同一软件的不同设置对于相位方向图的计算存在一定影响。在CST 微波工作室下扩展求解频率可以在一定程度上减小计算相位方向图的误差。而对于工作在L 波段的卫星接收天线而言,相位方向图均方根误差0.01mm 的精度可能已经超过了仿真软件对于相位方向图计算的误差限。参考文献[1] Tranquilla J M, Colpitts B G. ―GPS antenna design characteristics for high-precision applications‖[J]. Journal of Surveying Engineering, 1989, 115(1): 2-14.[2] IEEE Standard Definitions of Terms for Antennas Sponsored by Antenna Standards Committee of the IEEE Antennas and Propagation Society[3] John D. Kraus, ―Antennas‖ New York : McGraw-Hill, c1988. 2nd ed..pp 137-140[4] Investigation of antenna phase pattern by the electromagnetic simulation software, Ze Shen, Zhenxin Cao,2014 ICCP&HSIC[5] HFSS Help-Assigning boundaries-Assigning Radiation Boundaries;[6] 金建铭(著) 王建国(译), 电磁场有限元方法, 西安电子科技大学出版社,1998,P308~P317。[7] CST Help Content-Boundary Conditions[8] 王秉中, 计算电磁学. 科学出版社, 2002,第四章
 微信万人群1.各群不要重复加入2.仅限射频相关人员
微信万人群1.各群不要重复加入2.仅限射频相关人员
 加群主,注明:单位+方向射频百花潭关注中国最大的射频公众号
加群主,注明:单位+方向射频百花潭关注中国最大的射频公众号
 射频百花潭专注于射频微波/高频高速领域技术分享和信息传递。由资深射频专家、深圳兴森快捷射频实验室主任、《ADS2008/2011射频电路设计与仿真实例》《HFSS射频仿真设计实例大全》主编徐兴福建立,该号已40000人关注,10000人加群,博士2000人以上,包括IEEE Fellow多名。PCB制板、射频微波/高频高速PCB设计与仿真、技术咨询,请联系群主: 15989459034 xxf@chinafastprint.com。
射频百花潭专注于射频微波/高频高速领域技术分享和信息传递。由资深射频专家、深圳兴森快捷射频实验室主任、《ADS2008/2011射频电路设计与仿真实例》《HFSS射频仿真设计实例大全》主编徐兴福建立,该号已40000人关注,10000人加群,博士2000人以上,包括IEEE Fellow多名。PCB制板、射频微波/高频高速PCB设计与仿真、技术咨询,请联系群主: 15989459034 xxf@chinafastprint.com。

 可见在有限大的计算边界下,二元阵的相位方向图会因为计算边界大小而变化。当计算边界越大时,相位方向图的波动越小,其函数表达式约接近于无限大边界下的阶跃函数。
可见在有限大的计算边界下,二元阵的相位方向图会因为计算边界大小而变化。当计算边界越大时,相位方向图的波动越小,其函数表达式约接近于无限大边界下的阶跃函数。 3 理论与仿真计算半波阵子E 面相位方向图比较继而分析有限长度线源的相位方向图。令长度为d 的线源沿z 轴放置,坐标原点位于线源几何中心。那么在球坐标系下任一场点(X,Y,Z)距离线源上任一点(0,0,z)距离r1 可写作
3 理论与仿真计算半波阵子E 面相位方向图比较继而分析有限长度线源的相位方向图。令长度为d 的线源沿z 轴放置,坐标原点位于线源几何中心。那么在球坐标系下任一场点(X,Y,Z)距离线源上任一点(0,0,z)距离r1 可写作 那么由公式即可绘出半波阵子天线在不同计算半径r 下的E 面的相位方向图并与通过CST Microwave Studio, Feko Suite 与HFSS 三种仿真软件计算的相位方向图进行比较。仿真软件中的振子天线工作在L1 频段(1.575GHz)附近,振子臂半径为1mm,臂长经调节为41mm( 0.21入)。比较的结果如图4 所示。
那么由公式即可绘出半波阵子天线在不同计算半径r 下的E 面的相位方向图并与通过CST Microwave Studio, Feko Suite 与HFSS 三种仿真软件计算的相位方向图进行比较。仿真软件中的振子天线工作在L1 频段(1.575GHz)附近,振子臂半径为1mm,臂长经调节为41mm( 0.21入)。比较的结果如图4 所示。 可见于第二节中点源阵相位方向图随半径r 的变化趋势类似,线源天线理论计算的相位方向图波动也随着半径增大而减小。而由于理想的辐射边界应在形状上近似球面且在尺寸上尽量大,由图3 中可见,CST 软件计算得的相位方向图与理论计算在函数曲线上更为相似,这也印证了文章[3]的观点,即CST 的计算边界更近似于球面。通过CST,Feko与HFSS 软件计算得的相位方向图均方根误差分别为0.92°,0.31°与0.82°,在L1 频段分别对应长度为0.48mm,0.16mm 与0.43mm。由于在理想的无穷远边界下,半波阵子天线的E 面相位误差应趋于0。因此对于仿真软件计算得的E 面均方根误差可以认为是仿真软件造成的计算方向图的误差。因此将在下节中讨论如何减小这种仿真软件在相位方向图计算上的误差。4 仿真软件相位方向图计算误差产生分析在HFSS 软件中的辐射边界是用来模拟电磁波朝无穷远辐射的开放问题,而这类问题在天线设计中十分常见。一般使用的辐射边界采用第一阶吸收边界条件(ABC)[4]。文献[5]中的相应章节有对于该类边界条件的讨论,并给出该类吸收边界对于不同极化方式,不同入射角的电磁波的反射系数。而在CST 中计算辐射场则是使用的开放(openadd space)边界条件,[6]中说明该边界条件可以视作PML 边界加上了一些额外的空间用来计算远区场,并提到PML 层数为为取默认的四层就已足够。在[7]中则说明增加PML 层数可以使得局部和总体误差都单调地减小,但是PML 层数过多又会导致计算量的剧增。因此折衷考虑吸收边界效果与计算量,可以选取层数4 至8 层。因此通过调节CST 微波工作室仿真环境下半波阵子天线包括求解频率,计算边界大小(默认为计算频段中频波长的八分之一),PML 边界层数(默认为4 层)的计算设置,来比较天线E 面相位方向图在θ为10°~170°范围内的均方根误差,通过均方根误差值来比较不同设置下相位方向图的计算结果,并将均方根误差值对应到L1 频段波长。比较结果在表1 中给出。仿真采用时域求解器,在不同频率下计算的网格数单元数均为56400 个。
可见于第二节中点源阵相位方向图随半径r 的变化趋势类似,线源天线理论计算的相位方向图波动也随着半径增大而减小。而由于理想的辐射边界应在形状上近似球面且在尺寸上尽量大,由图3 中可见,CST 软件计算得的相位方向图与理论计算在函数曲线上更为相似,这也印证了文章[3]的观点,即CST 的计算边界更近似于球面。通过CST,Feko与HFSS 软件计算得的相位方向图均方根误差分别为0.92°,0.31°与0.82°,在L1 频段分别对应长度为0.48mm,0.16mm 与0.43mm。由于在理想的无穷远边界下,半波阵子天线的E 面相位误差应趋于0。因此对于仿真软件计算得的E 面均方根误差可以认为是仿真软件造成的计算方向图的误差。因此将在下节中讨论如何减小这种仿真软件在相位方向图计算上的误差。4 仿真软件相位方向图计算误差产生分析在HFSS 软件中的辐射边界是用来模拟电磁波朝无穷远辐射的开放问题,而这类问题在天线设计中十分常见。一般使用的辐射边界采用第一阶吸收边界条件(ABC)[4]。文献[5]中的相应章节有对于该类边界条件的讨论,并给出该类吸收边界对于不同极化方式,不同入射角的电磁波的反射系数。而在CST 中计算辐射场则是使用的开放(openadd space)边界条件,[6]中说明该边界条件可以视作PML 边界加上了一些额外的空间用来计算远区场,并提到PML 层数为为取默认的四层就已足够。在[7]中则说明增加PML 层数可以使得局部和总体误差都单调地减小,但是PML 层数过多又会导致计算量的剧增。因此折衷考虑吸收边界效果与计算量,可以选取层数4 至8 层。因此通过调节CST 微波工作室仿真环境下半波阵子天线包括求解频率,计算边界大小(默认为计算频段中频波长的八分之一),PML 边界层数(默认为4 层)的计算设置,来比较天线E 面相位方向图在θ为10°~170°范围内的均方根误差,通过均方根误差值来比较不同设置下相位方向图的计算结果,并将均方根误差值对应到L1 频段波长。比较结果在表1 中给出。仿真采用时域求解器,在不同频率下计算的网格数单元数均为56400 个。 可见,在CST 微波工作室仿真环境下,计算边界大小对于相位方向图计算结果并没有直接影响。增加PML 层数可以在一定范围内减小相位方向图的计算误差。同时相位方向图的计算结果与求解频率关系密切,扩展求解频率范围可以减小相位方向图的均方根误差,即令计算边界更接近于理想的辐射边界。同一天线模型在不同的求解频率下的均方根相差对应到距离可以达到0.75mm(编号1 与编号7 的数据)。经过仿真还发现增加网格单元数,对于相位方向图结果影响不大。5 结论不同仿真软件对于工作在L1 频段的半波振子天线相位方向图均方根误差的结果差值可以达到0.3mm。而在CST 微波工作室下的同一半波阵子天线模型,在不同的求解设置下对于相位方向图的均方根误差计算结果,相差可以达到0.75mm。可见不同仿真软件与同一软件的不同设置对于相位方向图的计算存在一定影响。在CST 微波工作室下扩展求解频率可以在一定程度上减小计算相位方向图的误差。而对于工作在L 波段的卫星接收天线而言,相位方向图均方根误差0.01mm 的精度可能已经超过了仿真软件对于相位方向图计算的误差限。参考文献[1] Tranquilla J M, Colpitts B G. ―GPS antenna design characteristics for high-precision applications‖[J]. Journal of Surveying Engineering, 1989, 115(1): 2-14.[2] IEEE Standard Definitions of Terms for Antennas Sponsored by Antenna Standards Committee of the IEEE Antennas and Propagation Society[3] John D. Kraus, ―Antennas‖ New York : McGraw-Hill, c1988. 2nd ed..pp 137-140[4] Investigation of antenna phase pattern by the electromagnetic simulation software, Ze Shen, Zhenxin Cao,2014 ICCP&HSIC[5] HFSS Help-Assigning boundaries-Assigning Radiation Boundaries;[6] 金建铭(著) 王建国(译), 电磁场有限元方法, 西安电子科技大学出版社,1998,P308~P317。[7] CST Help Content-Boundary Conditions[8] 王秉中, 计算电磁学. 科学出版社, 2002,第四章
可见,在CST 微波工作室仿真环境下,计算边界大小对于相位方向图计算结果并没有直接影响。增加PML 层数可以在一定范围内减小相位方向图的计算误差。同时相位方向图的计算结果与求解频率关系密切,扩展求解频率范围可以减小相位方向图的均方根误差,即令计算边界更接近于理想的辐射边界。同一天线模型在不同的求解频率下的均方根相差对应到距离可以达到0.75mm(编号1 与编号7 的数据)。经过仿真还发现增加网格单元数,对于相位方向图结果影响不大。5 结论不同仿真软件对于工作在L1 频段的半波振子天线相位方向图均方根误差的结果差值可以达到0.3mm。而在CST 微波工作室下的同一半波阵子天线模型,在不同的求解设置下对于相位方向图的均方根误差计算结果,相差可以达到0.75mm。可见不同仿真软件与同一软件的不同设置对于相位方向图的计算存在一定影响。在CST 微波工作室下扩展求解频率可以在一定程度上减小计算相位方向图的误差。而对于工作在L 波段的卫星接收天线而言,相位方向图均方根误差0.01mm 的精度可能已经超过了仿真软件对于相位方向图计算的误差限。参考文献[1] Tranquilla J M, Colpitts B G. ―GPS antenna design characteristics for high-precision applications‖[J]. Journal of Surveying Engineering, 1989, 115(1): 2-14.[2] IEEE Standard Definitions of Terms for Antennas Sponsored by Antenna Standards Committee of the IEEE Antennas and Propagation Society[3] John D. Kraus, ―Antennas‖ New York : McGraw-Hill, c1988. 2nd ed..pp 137-140[4] Investigation of antenna phase pattern by the electromagnetic simulation software, Ze Shen, Zhenxin Cao,2014 ICCP&HSIC[5] HFSS Help-Assigning boundaries-Assigning Radiation Boundaries;[6] 金建铭(著) 王建国(译), 电磁场有限元方法, 西安电子科技大学出版社,1998,P308~P317。[7] CST Help Content-Boundary Conditions[8] 王秉中, 计算电磁学. 科学出版社, 2002,第四章 微信万人群1.各群不要重复加入2.仅限射频相关人员
微信万人群1.各群不要重复加入2.仅限射频相关人员 加群主,注明:单位+方向射频百花潭关注中国最大的射频公众号
加群主,注明:单位+方向射频百花潭关注中国最大的射频公众号 射频百花潭专注于射频微波/高频高速领域技术分享和信息传递。由资深射频专家、深圳兴森快捷射频实验室主任、《ADS2008/2011射频电路设计与仿真实例》《HFSS射频仿真设计实例大全》主编徐兴福建立,该号已40000人关注,10000人加群,博士2000人以上,包括IEEE Fellow多名。PCB制板、射频微波/高频高速PCB设计与仿真、技术咨询,请联系群主: 15989459034 xxf@chinafastprint.com。
射频百花潭专注于射频微波/高频高速领域技术分享和信息传递。由资深射频专家、深圳兴森快捷射频实验室主任、《ADS2008/2011射频电路设计与仿真实例》《HFSS射频仿真设计实例大全》主编徐兴福建立,该号已40000人关注,10000人加群,博士2000人以上,包括IEEE Fellow多名。PCB制板、射频微波/高频高速PCB设计与仿真、技术咨询,请联系群主: 15989459034 xxf@chinafastprint.com。 相关文章:
- 仿真软件官方网址(05-08)
- 求高频仿真软件(05-08)
- 国内有什么类似CST的电磁仿真软件吗?(05-08)
- CST 宣布收购Flomerics 的整个电磁仿真软件产品线(05-08)
- 哪里可以下载ADS仿真软件(05-08)
- ADF仿真软件(05-08)
射频专业培训教程推荐











