采样和抗混叠滤波器浅述

摘要：在数据采样系统中，高于二分之一采样率的频率成分“混叠”(搬移)到有用频带。大多数时间，混叠是有害的副作用，所以在模/数(AD)转换级之前，将“欠采样”的较高频率简单滤除。但有时候，特意设计利用欠采样，混叠使得AD系统作为混频器工作。 本文讨论数据采样系统的不同滤波要求，介绍混叠以及用于抗混叠的不同类型滤波器。滤波是一种我们往往视为当然的常见过程。我们在打电话时，接收器滤除其它所有信道，使我们仅仅接收到特定的信道。当我们调节立体声系统的均衡器时，利用带通滤波器选择性增大或降低特定频带的音频信号。滤波器在几乎所有数据采样系统中扮演着重要角色。大多数模/数转换器(ADC)都安装有滤波器，滤除超出ADC范围的频率成分。有些ADC在其结构本身上就具有滤波功能。我们接下来讨论数据采样系统、滤波要求以及与混叠的关系。背景数据采样系统能够高精度处理的最大频率成分称为其奈奎斯特极限。采样率必须大于或等于输入信号最高频率的两倍。如果违反该规则，在有用频带内就会出现多余或有害的信号，称之为“混叠”。 例如，为了数字化1kHz信号，要求最低采样率为2kHz。在实际应用中，采样率通常较高，以提供一定的裕量，降低滤波要求。为帮助理解数据采样系统和混叠，我们以传统的电影摄影为例。在西部老片中，当马车加速时，车轮正常加速转动，然后看起来车轮速度却变慢了，再然后似乎停止了。当马车进一步加速时，车轮看起来像在倒转。实际上，我们知道马车没有倒走，因为其它动作都一切正常。什么原因造成了这种现象?答案就是：帧速率不够高，不足以准确捕获车轮的转动。为帮助理解，假设在马车车轮上贴一个看得到的标记，然后车轮转动。然后我们按时间拍摄照片(或采样)。由于电影摄影机通过每秒捕获一定数量的照片来捕获动作，所以本质上是数据采样系统。就像胶片采用车轮的离散图像一样，ADC捕获的是运动电信号的一系列快照。当马车首次加速时，采样率(电影摄影机的帧速率)远远高于车轮的转速，所以满足奈奎斯特条件。摄像机的采样率高于车轮转速的两倍，所以能够准确描述车轮的运动，我们看到车轮加速的样子(图1a和1b)。在奈奎斯特极限下，我们在180度范围内看到两个点(图1c)。人眼一般很难明确分辨这两个点的时间，这两个点同时出现，车轮表现为停止。在这种车轮转速下，转动速率是已知的(根据采样率)，但搞不清楚转动方向。当马车继续加速时，不再满足奈奎斯特条件，看到车轮的方式可能有两种：我们“看到”车轮在正转，其他人则看到是倒转(图1d)。

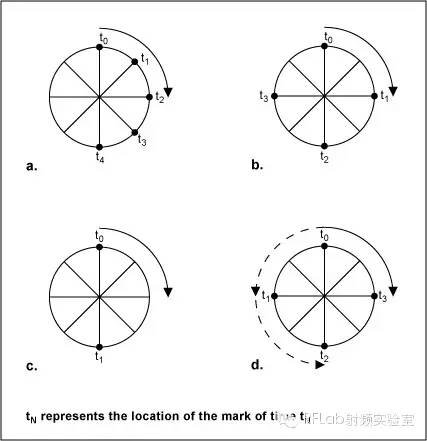图1. 马车车轮的例子这两种方向都可以看做是正确的方向，取决于您如何“看”车轮，但我们知道已经发生了信号混叠。也就是说，系统中出现了有害的频率成分，我们不能将其与真实值区分开，同时出现了正转和倒转的运动信息。我们一般看到倒转成分或正转成分的“约数”或“镜像”。由于是眼/脑相结合的方式处理数据,因此我们并不能察觉到车轮前转的主要信息。另一种有意思的现象是采样率与车轮转速严格相等时，由于标记始终出现在车轮的相同位置，所以数据几乎没有提供有用信息。在这种情况下，没有人能清楚车轮在转动还是静止。现在转入数学领域，假设车轮为单位圆，采用正弦和余弦坐标。如果在余弦值的正向和负向峰值采样(180度错相)，那么就满足奈奎斯特条件，能够利用两个采样数据点重构原始余弦值。所以，奈奎斯特极限是重构原始信号的关键。当增加的点越来越多时，复现原始信号的能力就提高了。转到频域，图2所示为采样数据系统的频率响应。注意，数据在采样率的倍数处重复(原始信号的“镜像”)；这是采样数据系统的一种基本特征。图2a中，满足奈奎斯特条件，有用频带内没有混叠现象。然而，在图2b中，由于有用频带内的最高频率大于二分之一采样率，不再满足奈奎斯特条件。重叠的区域发生了混叠；频率为fT的信号也出现在fT'处，与马车车轮的混叠相似。

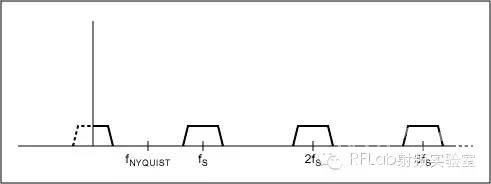图2a. 采样数据系统频率响应，无混叠

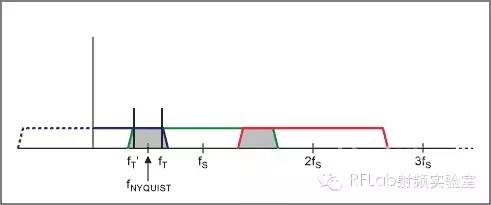图2b. 采样数据系统频率响应，发生混叠欠采样欠采样是一种功能强大的工具，可有效用于所选应用。欠采样允许ADC作为一个混频器，能够接收调制高频载波信号并产生较低频率的镜像。这种方式下，就像下变频器。另一种主要优点是允许ADC的采样率低于奈奎斯特频率，一般具有较明显的成本优势。例如，假设调制载波为10MHz，带宽为100kHz (±50kHz，中心频率为10MHz)。以4MHz进行欠采样，产生1阶和与差项(f1 + f2和f1 - f2)，分别为14MHz和6Mz；2阶项(2f1、2f2、2f1 + f2、f1 + 2f2、| 2f1 - f2 |、| f1 - 2f2 |)，分别为8MHz、20MHz、18MHz、2MHz、24MHz和16MHz。出现在2MHz处的镜像信号为有用信号。注意，我们的原始信号在10MHz，通过对其进行数字化在2MHz产生了镜像。现在，我们可以在数字域进行信号处理(滤波和混频)，恢复原始50kHz信号。该过程无需大幅的模拟处理，这是其主要优势之一。由于所有处理都在数字域完成，如果需要对电路的性能和特性进行更改，只需修改软件即可。相对而言，对于模拟设计，如果需要更改电路性能，需要改变电路硬件元件和布局，并且成本相当高。欠采样的一项缺点是有用频带内可能出现有害信号，您不能将其与有用信号区分开。此外，欠采样时，ADC输入的频率范围往往非常宽。在上例中，即使采样率为4MHz，ADC前端仍然必须采样10MHz信号。相对而言，如果在ADC之前利用模拟混频器将调制载波信号向下搬移到基带，那么ADC的输入带宽只需要为50kHz，而非4MHz，降低了ADC前端和输入滤波要求。

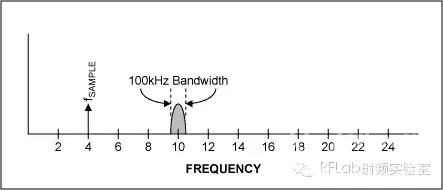图3a. 欠采样示例

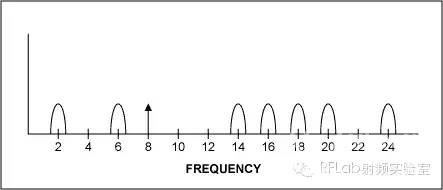图3b. 欠采样数字化的镜像信号(1阶和2阶)过采样过采样提供所谓的处理增益。在过采样时，以较高采样频率获得多出实际需要的采样数量，然后对数据滤波，从而有效降低系统的噪底(假设噪声为宽带白噪声)。这不同于平均，后者是获取很多采样，噪声被平均。可以这么理解过采样：如果输入信号来自于扫描频率的信号源，频谱则可以分为多个范围或“容器”，每个容器的带宽固定。宽带噪声分散在整个有用频率范围内，所以每个容器具有特定量的噪声。现在，如果提高采样率，那么频率容器的数量也增多。在这种情况下，出现的噪声量仍相同，但我们有更多的容器可供容纳噪声。然后我们利用滤波器滤除超出有用频带的噪声。结果就是每个容器的噪声减少，所以就通过过采样有效降低了系统的噪底。举例说明，如果我们有一个2ksps ADC (下式中使用1kHz奈奎斯特极限)和1kHz信号，ADC之后为1kHz数字滤波器，处理增益由下式给出：-10 × log (1kHz/1kHz) = 0dB。如果们将采样率增大至10ksps，处理增益现在为-10 × log (1kHz/5kHz) = 7dB，或者说大约1位分辨率(1位大约相当于信噪比(SNR)提高6dB)。通过过采样，噪声没有减少，而是分散在更宽的带宽内；将部分噪声置于有用带宽范围之外，效果就相当于减少了噪声。这种噪声改善基于以下公式：SNR改善(dB) = 10 × LOGA/B，其中A等于噪声，B等于过采样噪声。表述这一过程的另一种方式是：过采样降低了带内RMS量化噪声，系数为过采样率的平方根。或者，如果噪声降低二分之一，则相当于3dB有效处理增益。不要忘了，我们这里仅讨论了宽带噪声。过采样不能简单消除其它噪声源和其他误差。抗混叠滤波器有了以上背景知识后，我们现在讨论抗混叠滤波器。在选择滤波器时，目标是提供一个截止频率，能从ADC输入中消除有害信号或至少将其衰减至不对电路形成负面影响。抗混叠滤波器是满足这一要求的低通滤波器。如何选择正确的滤波器?需要考虑的关键参数是在通带内的衰减量(或纹波)、阻带内的预期滤波器滚降、过渡区域的陡度，以及不同频率通过滤波器时的相位关系(图4a)。

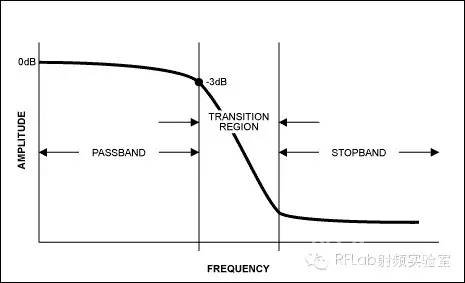图4a. 实际滤波器理想滤波器具有“砖墙”响应(图4b)，也就是说其过渡比是无限大的。然而，在实际应用中不可能存在这种情况。滚降越陡，滤波器的“Q”或品质因子越高；Q因子越高，滤波器的设计就越复杂。较高的Q因子会造成滤波器不稳定以及在相应的拐点频率下自振。选择滤波器的关键是了解干扰信号的频率及对应幅值。例如，对于手机，设计者知道邻近信号的最差工作条件幅值和位置，从而有针对性地进行设计。并不是所有信号都能在频域预测，甚至有些已知干扰信号太大，不能足够地衰减。但是，根据环境和应用，您可考虑已知干扰和设计，最大程度降低随机干扰，确保工作更可靠。

图4b. 理想滤波器已知有用信号频率后，利用简单的滤波程序确定所需的滤波器结构，以满足通带、阻带和过渡区域要求。在四种基本滤波器类型中，每种都有其各自的优势(图5)。

图5. 四种基本的滤波器类型例如，巴特沃斯(Butterworth)滤波器的通带区域最平坦，意味着在相应频率范围内的衰减最小；贝塞尔(Bessel)滤波器的滚降较平缓，但其主要优势是线性相位响应，意味着每种频率成分在通过滤波器时的延时是相等的；由于群延迟定义为相位响应相对于频率的偏差，所以线性相位响应通常指的是固定群延迟。切比雪夫(Chebyshev)滤波器的滚降较陡，但在通带内纹波较大。椭圆(Elliptic)滤波器的滚降最陡。对于最简单的抗混叠滤波器，简单的单极点无源RC滤波器往往是可以接受的。在其它情况下，有源滤波器(即使用运放)比较合适。有源滤波器的一项优势是多阶滤波器，滤波器对外部元件值不太敏感，特别是滤波器的“Q”值。抗混叠滤波器通常不必严格对应拐点频率的位置，所以设计时具有一定余地。例如，如果您需要最大平坦度，但在通带内仍然有太大衰减，只需将拐点频率移远即可解决问题。如果阻带衰减太小，则可提高滤波器的极点数。另一种方案是在滤波后将信号放大，提高信号相对于有害信号的幅值。Maxim具有多种低功耗、低通滤波器可供选择，可用于抗混叠；其中包括MAX7490通用开关电容滤波器、MAX740x/MAX741x家族尺寸最小的低功耗低通开关电容滤波器，以及MAX274/MAX275通用连续时间方式滤波器。Maxim也提供丰富的低功耗高精度运放，适用于希望自己设计滤波器的用户。对于这些用户，强烈推荐在设计过程中参考好的滤波器手册。本文来源:Maxim官网