ADS仿真反射系数

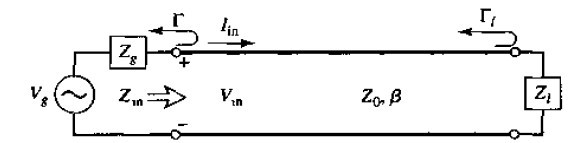
请教大家一个问题,根据反射系数的计算公式:gama=(Zin-Zg)/(Zin+Zg);此处Zg是源阻抗,ZL是负载阻抗,Z0是传输线特性阻抗,Zin是负载通过传输线变换到源端的阻抗
当Zg与输入阻抗Zin相等的时候就没有反射(其中Zg和Zin都可为复数),微波工程等书上也是这样讲述的,但是在ADS中仿真的时候,2个term要设置成共轭的时候反射才为0,相等的时候反而有反射,这是为什么?
谁说短路的时候反射系数一定为-1?
归一化到实数当然只能等于-1,归一化到复数阻抗(假设源是复数阻抗的),反射系数可以等于其它模值为1,角度不为-180度的值。
很久没有上网,才看到你的回复。
1.105a里面也是 因为是实数,所以才省略了共轭。
能找到的所有 省略共轭 的公式里,都是Z0 这个实数。
讨论复数的时候都是加了共轭的。
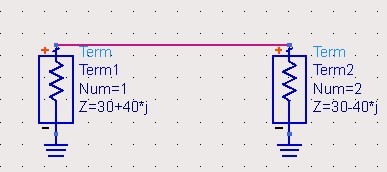
ads里面根据你的设置算的是传输系数,当然共轭的时候好了,你现在要算的是源和端口的匹配,包括上面的公式都是源端匹配公式,这个不能用这个模型来算,要用ads中的史密斯原图工具来算。
貌似,电路分析基础里面教育我们,输入输出共轭时才能实现最大功率传输。这里说的阻抗相等,我认为应该是指实部相等。
我觉得在ADS里面,Term1表示信号源,阻抗是从负载看向源端的阻抗, term2表示负载,阻抗是从源看向负载的阻抗,当两者匹配时,是共轭的关系。
我觉得书本里面没有清楚的说明Zl是如何定义的,如果term2的阻抗是指从负载看向源端的阻抗,当两者匹配时,那么term2的值就是30+40j,和term1的阻抗相等。
我想ADS和书本都正确,只是大家潜在的定义不同。
但是在pozar的微波工程和西电的微波技术基础那2本书中,如上图2.77式那样,Zin和Zg都是复数,并没有限定是实数,并且前后文也都说明了Zin和Zg都是复数,总反射系数的公式也是2.77式,这样得到总反射系数为零的条件就是Zin和Zg相等而不是共轭,难道是这2本书上都有错误? 书上也说了总反射为0的时候负载得到的功率不一等最大,共轭匹配时负载得到功率最大但总反射系数不一定为0
我现在要计算的是从源端向后看总的反射系数,不是源到传输线的反射系数,就应该用源阻抗Zg和负载阻抗通过传输线变换到源端的阻抗Zin来计算吧?和上图我给出的ADS仿真模型应该是一致吧,应该此时仿真出来的也是term1端口总的反射系数吧?书上也明确给出了此时总反射系数的计算公式是gama=(Zin-Zg)/(Zin+Zg), 并且书上的情况也是Zin和Zg都是复数,这样总反射系数为0的条件就应该是Zin和Zg相等而不是共轭吧?难道2本书上都写错了?
你应该看一下2.6节最开始的假设,即传输线是无耗的,这就说明Z0一定是实数;而且你的第一个贴图里边说的源和负载线匹配就是指的相等,而此时书上得出的结论是没有实现最大功率传输,因为在负载端仍然存在反射,也就是说能量以驻波的形式留在了传输线上;2.6.3节才给出了共轭匹配能得出最大功率传输的情况。
是的,Z0一定是实数,但是Zin就不是实数了,负载端存在反射,源和传输线间也有反射,但是总的反射系数为0,也就是从源端向后看总的反射系数为0(相当于负载端反射与源和传输线间的反射抵消了)
而按书上的说法总的反射系数为0的条件就是Zin=Zg,而不是共轭
仿真不会有问题的。就是上图,或者中间加一段传输线也可以,但源端阻抗就应该设置成负载经过传输线后变换到的阻抗Zin,此时S11是不为0的,要设置成共轭是才为0
Zg是源阻抗,ZL是负载阻抗,Z0是传输线特性阻抗,Zin是负载通过传输线变换到源端的阻抗
最大功率传输的条件和总反射系数为0的条件不一样,最大功率传输时,总的反射系数可能不为零,总反射系数为0时,也可能得不到最大功率,我现在问的是总反射系数为0的条件
因为小编并没有给全相应的信息,在此仅做以下估计:
1.公式中的阻抗定义,gama=(ZL-Z0)/(ZL+Z0)中的Z0是端口的特征阻抗,此时只应用在行波传输的情况下,并且和电磁波的模式相关。在绝大部分的应用中,此处的Z0应换为Zref,为端口的参考阻抗(人为定义,方便起见,通常为实数,50ohm)。再详细解释就很麻烦了,详见微波工程这本书吧。
2.Term中的那个阻抗Z在S参数仿真时,定义为端口参考阻抗Zref,没有涉及S参数仿真时为一复负载。
4.小编给出的电路,如果是S参数仿真,计算得到的结果是一个短路点的S矩阵,只是相应的两个端口参考阻抗不同。
5.貌似ADS中使用的是功率波的定义(power wave),(此处我不太确定,但仿真结果与此吻合),该定义在参考阻抗为是实数时问题不大,当参考阻抗是复数时,该定义就完全失去了物理意义,成为纯数学公式。
6.根据功率波的定义,gama=(ZL-Zref^*)/(ZL+Zref),注意分子上是参考阻抗的共轭。因此会出现小编的仿真结果。
7.在功率波的定义下,如果参考阻抗是复数,对短路点求得的反射系数都不会是我们所认为的 -1。
所有书上给出总反射系数计算的公式为:gama=(Zin-Zg)/(Zin+Zg);此处Zg是源阻抗,ZL是负载阻抗,Z0是传输线特性阻抗,Zin是负载通过传输线变换到源端的阻抗,参见pozar 微波工程 或者西电 微波技术基础,而且书上的情况Zin和Zg也是复数,
然后ADS中仿真时,如果把term1换为一个带内阻的电压源,该内阻等于Zg,然后term2和源之间可以加一段特性阻抗为Z0的传输线,计算出负载通过传输线变换到源端口的阻抗Zin,此时按照书上的公式应该是Zg=Z0时总的反射系数为0,但是ADS中仿真却是Zg=Zin的共轭时反射系数才为0
12楼的意思是ADS中仿真的反射系数定义和书上不一样?
好吧,首先,什么是反射系数?
最根本的 gamma=b/a
那么这里的a和b的定义又是什么?
本质上,a和b应该对应于行波(travelling wave),相应的为特征阻抗(波阻抗)。
然而实际中,基于不同的测量方法,测到的是行波叠加的结果,也就是说a和b是伪波(pseudo wave),对应为参考阻抗。
如果你把微波工程从头开始看,会发现个中奥妙。
然而貌似各种书上都是功率波的定义(power wave),该定义在参考阻抗是实数时和伪波区别不大,差别出现在复参考阻抗的情况。功率波根本就是一个数学结构,和实际联系不大。
关于你说的第七点,ADS中对短路点求得的反射系数恰恰是按你说的第六点来计算的,所以不是-1,所以貌似ADS中gama=(Zin-Zg^*)/(Zin+Zg);
但是书上的gama=(Zin-Zg)/(Zin+Zg),这个公式是通过反射波比入射波推导出来的,推导过程中并没有要求Zin或Zg是实数?
好吧,反射波和入射波的定义是什么?如果a是入射波,b是反射波,最原始的 gamma=b/a,就是我上个回帖中提到了。
一般常见的所谓入射波,反射波或者电压波,都是基于功率波的定义,下面引用wiki上的这个定义:
http://en.wikipedia.org/wiki/Scattering_parameters
注意里面反射波 b 的定义,用的是Zp的共轭,这个定义只能这样,要不在Zp为复数时无法计算功率。这个定义无法回避当负载短路时,Zp为复数, gamma 不等于 -1。然而所有的所谓入射波,反射波或者电压波都是基于这个定义,因此,Zp为实数成了一个前提条件。
事实上,该定义仅仅是一个数学模型,无法准确描述波的概念。只是当Zp为实数时,结果与真正意义上的波吻合而已。
对于电磁波来说,只有在TEM模下,才有比较明确的电压及阻抗概念,对于TE,TM或者其他合成模,电压及阻抗都是很模糊的,微波工程里面对此描述的比较清楚。
然而,在微波工程第二章里,Z0都简化成实数了。
不过这个结果gama=(Zin-Zg)/(Zin+Zg) 是适用于真正意义上的波量的,无所谓Zin,Zg的虚实,(Zg在这里是参考阻抗或特征阻抗)。
多谢细心解答,讨论了半天,还是有点模糊,貌似就是gama=(Zin-Zg)/(Zin+Zg) 这个公式是对的?ADS中用共轭的公式有其局限性,所以在复数参考阻抗下不正确?但是由于实际电路都是按最大功率来匹配的,也就是共轭匹配,所以设计是就按共轭匹配来做就对了吧。
这个公式gama=(Zin-Zg)/(Zin+Zg)当然是对的,对应于波量。
ADS中用的公式我不确定,即便是另外一个,也不能说错,仅仅是不同的数学表达而已。
最根本的,使用一个实数作为参考阻抗,尽量避免以上问题,而且在绝大多数情况下都适用。在实数条件下,各种描述都趋于统一。
但是在设计的时候源内阻Zg很多情况下都是复数,但是貌似所有设计都是要求最大功率,所以用共轭匹配,并没见过要求总反射系数为0的匹配要求,倒是避免了这一实际问题。
顶一个!
匹配分弱匹配和强匹配,共扼匹配就是强匹配(线上有反射波的。;
弱匹配:
源与线:(信号源处无反射波)
或负载与线匹配(负载处无反射波)。
没有加共轭的公式都是不严密的公式。
况且,人家pozar从来没有用过不加共轭的公式,他以前书里面都是Z0,因为Z0是50ohm所以才不用加共轭符号。
下图是pozar微波工程最新的第4版的,在P186页,他专门强调这个公式里面的共轭的问题!
结论就是必须要加共轭,ADS是对的。
多谢,找到出处了,非常感谢
那你如何解释,这个第4版中公式1.105a?(29页)
在这个式4.63中,反射系数任然源于最原始的定义,b/a。
只是因为功率波的b的定义里面有个共轭而已。注意这个公式所处的小节“Power Waves and Generalized Scattering Parameters”。
同时需要注意的是,这里不仅用了功率波,还引入了电压和电流。把电磁场转换成电流电压的表达是有严格条件的,比如TEM和无损。在这些严格条件下,Z0只能是实数。
Pozar建议选择参考阻抗的方法,也解决不了这个功率波定义的致命伤。当ZL=0时,反射系数是多少?ZR=ZL^*=0, GammaP=0/0=?
楼上又把我绕迷糊了,你意思是23楼的公式也不是严谨的?那准确的公式是什么?
?
很久没有上网,才看到你的回复。
1.105a里面也是 因为是实数,所以才省略了共轭。
能找到的所有 省略共轭 的公式里,都是Z0 这个实数。
讨论复数的时候都是加了共轭的。
谁说短路的时候反射系数一定为-1?
归一化到实数当然只能等于-1,归一化到复数阻抗(假设源是复数阻抗的),反射系数可以等于其它模值为1,角度不为-180度的值。
相关文章:
- ADS Momentum 仿真设计流程(英文)(05-08)
- 仿真软件官方网址(05-08)
- 软件中的耦合问题仿真(05-08)
- 请高手看看这几个错误,你们在仿真过程遇到没有啊,请指教谢谢!(05-08)
- 仿真时在30GHz, lumped port 问题(05-08)
- 仿真时出现的问题,请教大家!(05-08)











