CST的主要算法及2009版的新增内容
05-08
1) CST 的主要算法
软件的基本算法决定了软件的处理能力,CST MWS 采用业界最先进的电磁场全波时域仿真算法――有限积分法(FIT),对麦克斯韦积分方程进行离散化并迭代求解,可对通信、电源、电气和电子设备等系统复杂的电磁场耦合、辐射特性、EMC/EMI 进行精确仿真。从数学上可以证明,在众多的电磁场数值算法中,唯有有限积分法拥有且仅拥有解析麦克斯韦方程组所拥有的全部结论!如:不会有磁核、增根等非物理的结果出现。
下图展示了有限积分法为解析到网格的一一映照。
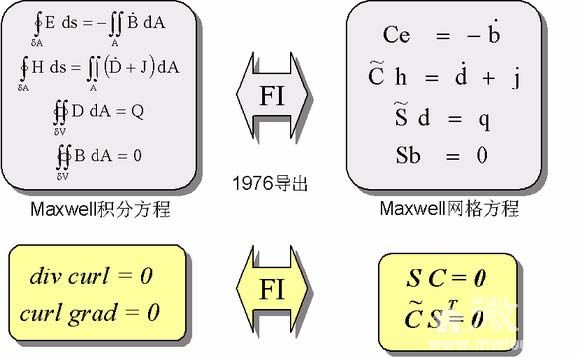
CST MWS 所采用的时域算法FIT,只须一步步迭代求解,不用进行矩阵求逆。此内在特性决定了,在32 位计算机上,适合的仿真结构涵盖电小、电中和电大,电尺寸从1/10 波长,几个波长,数十波长到一百多个波长,均可取得良好的表现。在64 位计算机上最高仿真电尺寸可到数百波长。
下图显示了时域算法和频率算法对CPU 时间和内存需求的数学原理。
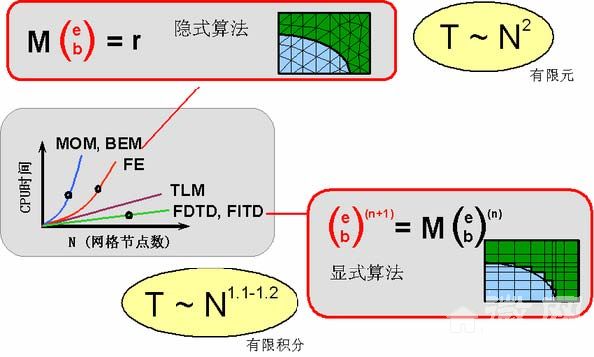
由数学结论可知,体矩量法、有限元法和有限积分法三者的计算量(体现在CPU 时间和所需内存)分别正比于所分网格数N 的3 次、2 次和1.1-1.2 次方。当结构的电尺寸比较大或比较复杂,网格点则逐渐增大,对于目前主流的32 位计算机(2GBytes 内存/2.6GHz 主频/单CPU)来说,前两者将不再能够胜任。这个网点数分别在几万和几十万。而有限积分法则可处理800 万点,约8 小时CPU 完成十几到数十个倍频程的全部仿真。这个快速宽带仿真特点归功于有限积分法的显式时域算法。
另一方面,三者的仿真速度是由各自算法所决定的。换言之,即便是采用64 位计算机,它们三者的速度的相对关系是不会改变的。有些人错误地认为,64 位机能够提高速度,其实是64 位机由于它们的寻址空间大大地增加2 CST 工作室套装™–常见问题解答FAQs便可以“接受”大网格点的仿真问题了,不像32 位计算机有2-3GBytes 最大可接受文件的限制。可是,“接受”或能够仿真绝不意味着它们的计算速度就提高了。其实,原来固有的N3、N2 和N1.1-1.2 的计算量依然不变,即所需的CPU 时间同样还是这么多。举例来说,对于有限元方法,10 万个网格点若需要10 小时CPU,则100 万点时则需1000 小时!这个N 平方关系与32 位还是64 位计算机无关。内存需求同样满足N 的平方关系。故导致100 万个网格点32 位机无法计算,但64 位机则可以,只要其物理内存足够的大。这就是计算速度及内存需求与网格点关系的通用解释。请注意:CPU 数目的增加一般是线性的(目前主流64 位PC 工作站最大支持16 个CPUs)。况且,它还受到硬件投资的约束。
再看对计算机的要求。CST MWS 由于采用有限积分算法,在数学上没有矩阵求逆的过程,而有限元法是必须要做矩阵求逆,所以对计算机配置要求比较低,具体在CPU P4,内存64M,硬盘1G 以上即可。举一个具体例子,一个普通计算机,配置是CPU P4 2GHz,内存1G,硬盘1G 的计算机,可计算分析800 万个网格的大物体;而同样配置下,有限元软件不超过20 万个网格。
2) CST MWS 的专有技术
CST MWS 专有的PBA 和TST 技术,在保证精度的情况下,极大的降低了内存需求,提高计算速度。1998 年引入了专有的PBA™(Perfect Boundary Approximation™)技术,使CST MWS 的结构逼近趋近完美。此方法采用插值的方式,弥补了经典FDTD 类算法对曲面物体近似度差的缺点,同时又保有网格划分容易、对大问题快速及内存需求小这三大原有的优点。2002 年又引入了TST™(Thin Sheet Technology™)薄片技术,在程序内部,通过对细线和薄片的专门处理,大大地提升了对这两类问题的仿真度,使得软件不但速度快,内存需求低,而且精度高。最新的版本,对TST™技术内部又有所改进,从此对于某些特殊问题,如共形天线,不用特殊的处理,就可以算到很精确。2004 年引入了MSS™(Multilevel Subgridding Scheme™)多级子网技术,使网格定义更为有效经济,大大地减少了网格点,从而提供了仿真速度。
CST MWS 在新版本中,软件在保持原有特点的情况下,重新对子网格进行了整理和优化,使这一专利技术更加成熟和灵活。软件拥有多层子网格自动嵌套技术,软件可以根据物体结构的变化,网格可在计算区域内任意中止,自动使用子网格优化技术,这一灵活的局部子网极大地提高了运算速度和极大减少了对计算机的资源占有。
在新版本中,CST MWS 软件已经引入了积分方程法(矩量法)和多层快速多极子算法(MLFMM),使电大尺寸的计算速度得到彻底提高。这个算法可以在物体的表面进行网格剖分。
3) 两种算法的结合
CST 全波时域仿真算法——有限积分法(FIT)和多层快速多极子算法都集成在CST 一个界面下,这两种算法各有特点,有限积分法是属于全波分析方法,可以处理任意结构、任意材料的物体,也可以得到任意想要的结果。多层快速多极子算法是处理物体的面网格,对物体不是进行体网格剖分,只在物体的表面划分网格,这种网格决定了它在处理结构复杂,多层介质等方面是不足的,但他在解决结构简单的电大问题时很有效。CST 微波工作室同时拥有这两个完全不同算法,可以互补使用。
4) CST 2009 版的新特点
下列表格展示了CST 2009 版本的新特点。更多新特点的细节可以参见 CST STUDIO SUITE™ 2009 的产品介绍,或者查看在线help。




软件的基本算法决定了软件的处理能力,CST MWS 采用业界最先进的电磁场全波时域仿真算法――有限积分法(FIT),对麦克斯韦积分方程进行离散化并迭代求解,可对通信、电源、电气和电子设备等系统复杂的电磁场耦合、辐射特性、EMC/EMI 进行精确仿真。从数学上可以证明,在众多的电磁场数值算法中,唯有有限积分法拥有且仅拥有解析麦克斯韦方程组所拥有的全部结论!如:不会有磁核、增根等非物理的结果出现。
下图展示了有限积分法为解析到网格的一一映照。

CST MWS 所采用的时域算法FIT,只须一步步迭代求解,不用进行矩阵求逆。此内在特性决定了,在32 位计算机上,适合的仿真结构涵盖电小、电中和电大,电尺寸从1/10 波长,几个波长,数十波长到一百多个波长,均可取得良好的表现。在64 位计算机上最高仿真电尺寸可到数百波长。
下图显示了时域算法和频率算法对CPU 时间和内存需求的数学原理。

由数学结论可知,体矩量法、有限元法和有限积分法三者的计算量(体现在CPU 时间和所需内存)分别正比于所分网格数N 的3 次、2 次和1.1-1.2 次方。当结构的电尺寸比较大或比较复杂,网格点则逐渐增大,对于目前主流的32 位计算机(2GBytes 内存/2.6GHz 主频/单CPU)来说,前两者将不再能够胜任。这个网点数分别在几万和几十万。而有限积分法则可处理800 万点,约8 小时CPU 完成十几到数十个倍频程的全部仿真。这个快速宽带仿真特点归功于有限积分法的显式时域算法。
另一方面,三者的仿真速度是由各自算法所决定的。换言之,即便是采用64 位计算机,它们三者的速度的相对关系是不会改变的。有些人错误地认为,64 位机能够提高速度,其实是64 位机由于它们的寻址空间大大地增加2 CST 工作室套装™–常见问题解答FAQs便可以“接受”大网格点的仿真问题了,不像32 位计算机有2-3GBytes 最大可接受文件的限制。可是,“接受”或能够仿真绝不意味着它们的计算速度就提高了。其实,原来固有的N3、N2 和N1.1-1.2 的计算量依然不变,即所需的CPU 时间同样还是这么多。举例来说,对于有限元方法,10 万个网格点若需要10 小时CPU,则100 万点时则需1000 小时!这个N 平方关系与32 位还是64 位计算机无关。内存需求同样满足N 的平方关系。故导致100 万个网格点32 位机无法计算,但64 位机则可以,只要其物理内存足够的大。这就是计算速度及内存需求与网格点关系的通用解释。请注意:CPU 数目的增加一般是线性的(目前主流64 位PC 工作站最大支持16 个CPUs)。况且,它还受到硬件投资的约束。
再看对计算机的要求。CST MWS 由于采用有限积分算法,在数学上没有矩阵求逆的过程,而有限元法是必须要做矩阵求逆,所以对计算机配置要求比较低,具体在CPU P4,内存64M,硬盘1G 以上即可。举一个具体例子,一个普通计算机,配置是CPU P4 2GHz,内存1G,硬盘1G 的计算机,可计算分析800 万个网格的大物体;而同样配置下,有限元软件不超过20 万个网格。
2) CST MWS 的专有技术
CST MWS 专有的PBA 和TST 技术,在保证精度的情况下,极大的降低了内存需求,提高计算速度。1998 年引入了专有的PBA™(Perfect Boundary Approximation™)技术,使CST MWS 的结构逼近趋近完美。此方法采用插值的方式,弥补了经典FDTD 类算法对曲面物体近似度差的缺点,同时又保有网格划分容易、对大问题快速及内存需求小这三大原有的优点。2002 年又引入了TST™(Thin Sheet Technology™)薄片技术,在程序内部,通过对细线和薄片的专门处理,大大地提升了对这两类问题的仿真度,使得软件不但速度快,内存需求低,而且精度高。最新的版本,对TST™技术内部又有所改进,从此对于某些特殊问题,如共形天线,不用特殊的处理,就可以算到很精确。2004 年引入了MSS™(Multilevel Subgridding Scheme™)多级子网技术,使网格定义更为有效经济,大大地减少了网格点,从而提供了仿真速度。
CST MWS 在新版本中,软件在保持原有特点的情况下,重新对子网格进行了整理和优化,使这一专利技术更加成熟和灵活。软件拥有多层子网格自动嵌套技术,软件可以根据物体结构的变化,网格可在计算区域内任意中止,自动使用子网格优化技术,这一灵活的局部子网极大地提高了运算速度和极大减少了对计算机的资源占有。
在新版本中,CST MWS 软件已经引入了积分方程法(矩量法)和多层快速多极子算法(MLFMM),使电大尺寸的计算速度得到彻底提高。这个算法可以在物体的表面进行网格剖分。
3) 两种算法的结合
CST 全波时域仿真算法——有限积分法(FIT)和多层快速多极子算法都集成在CST 一个界面下,这两种算法各有特点,有限积分法是属于全波分析方法,可以处理任意结构、任意材料的物体,也可以得到任意想要的结果。多层快速多极子算法是处理物体的面网格,对物体不是进行体网格剖分,只在物体的表面划分网格,这种网格决定了它在处理结构复杂,多层介质等方面是不足的,但他在解决结构简单的电大问题时很有效。CST 微波工作室同时拥有这两个完全不同算法,可以互补使用。
4) CST 2009 版的新特点
下列表格展示了CST 2009 版本的新特点。更多新特点的细节可以参见 CST STUDIO SUITE™ 2009 的产品介绍,或者查看在线help。




2009有很多功能都不知道是做什么用的
我还没用过,不过对于一般的设计我想可能基本用不上的
还是增加了一些功能,有些功能不知道做的怎么样,比如热分析中的瞬态分析是否可以像ug或其它专门的热分析软件一样功能强大,集成太多,往往会造成都不是特别专,希望这一点能有所改变
thank you !
真是长知识了
学习了!
Ding~
好东西,学习了!
相关文章:
- HFSS中的迭代算法(05-08)
- 功放设计中会用到哪些算法(05-08)
- CST算法理论(05-08)
- HFSS优化大家一般用哪种算法呢?(05-08)
- 求助:CTS中优化算法能否自定义(05-08)
- 遗传算法调用HFSS进行优化计算(05-08)
射频专业培训教程推荐











