Technical Notes > Radiated Fields > Array Factors
Regular Uniform Arrays
Let us define a uniform array as an array with unity
amplitude weights for all elements, i.e., An
= 1 for all n. For the case in which a uniform
array is scanned to direction ![]() ,
the array factor (eq.
2) becomes
,
the array factor (eq.
2) becomes
|

|
(6) |
For a "regular" uniform array with element spacing defined by lattice vectors u and v, the element position vectors rn may be written in the doubly-indexed form
with m
= 1, 2, ..., Nu and n
= 1, 2, ...., Nv. The
total number of elements in the array is given by
N = NuNv.
The array factor (eq. 6) for the Nu
x Nv
![]() array becomes
array becomes
|
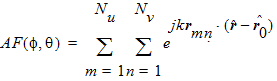
|
(8) |
-

国内最全面的HFSS培训课程,包含7套视频教程和2本教材,资深专家讲解,视频操作演示,结合最新工程案例,让HFSS学习不再难...【详细介绍】





