• 首页
• HFSS教程
• ADS教程
• CST教程
• 射频工程师培训
• 微波仪器操作培训
• 天线设计培训
• 射频专业基础课

Ansoft Designer / Ansys Designer 在线帮助文档：

Nexxim Simulator >
Nexxim Time-Varying Noise Analysis >
   TV Noise Technical Notes       

TV Noise Technical Notes

Sources of Noise

The noise output Onoise is a combination of thermal, shot, and flicker noise.

Thermal noise is a variation in current due to random thermal motion of the electrons in physical resistors and bulk materials. Thermal noise is directly proportional to the absolute temperature.

Shot noise is a fluctuation in the current across P-N junctions in diodes and transistors due to random barrier crossings by electrons and holes in the vicinity of the junction. Shot noise is associated with a direct current flow.

Flicker noise is a random variation in current associated with contamination and crystal defects in semiconductors. Like shot noise, flicker noise is associated with a flow of direct current. Flicker noise generates a noise signal with energy concentrated at low frequencies; because of this 1/f frequency dependence, flicker noise is also called 1/f noise.

Noise Spectrum

The noise spectrum consists of the power spectrum of the coefficients for the harmonic frequencies.

The large-signal periodic steady-state of a circuit can be represented by the Fourier equation derived in harmonic balance. In a single large-signal circuit, the one-tone periodic steady state transfer function can be represented by the equation: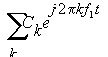

Where k is the harmonic number , f₁ is the large-signal steady-state frequency, and C_k is the coefficient giving the magnitude of the function at harmonic k.

The small-signal AC perturbation can be represented by the equation: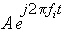

Where A is a constant and f_i is the small-signal frequency.

The output response of the circuit is the product of the small-signal perturbation and the large-signal transfer function. The response can be represented by the equation: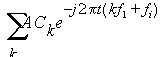

The frequency of the response has been shifted by f_i. When constant A is normalized to 1 (one), the coefficient C_k gives the magnitude of the response at harmonic k.

In a circuit with two large-signal tones f₁ and f₂, the periodic steady state can be represented by the equation: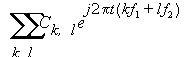

Where k is the harmonic number for frequency f₁ and l is the harmonic number for frequency f₂. The response of this circuit to the small-signal perturbation above can be represented by the equation: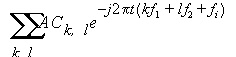

The frequency of the response has again been shifted by f_i. When constant A is normalized to 1 (one), the coefficient C_k,l gives the magnitude of the response at the frequency that combines harmonic k of f₁ and harmonic l (letter l) of f₂.

Noise Computation Formulas

The calculation of the noise frequencies is a multi-step procedure.

First, a set of output frequencies is generated from the swept output frequencies by applying the offsets from the RELHARMVEC list to the (n) corresponding frequencies from the SS_TONES list.

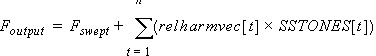
Here is an example that shows how the offsets work.

Suppose the desired output frequencies are 1001Hz, 1010Hz, and 1100Hz. This sequence could be specified using the POI sweep specification. However, this example uses the RELHARMVEC offset to calculate the desired frequencies. (Since only one offset is required, the example could use RELHARMNUM instead of RELHARMVEC.)

.TV_NOISE
+ DEC 1 1 100
+ SS_TONES=[1000]
+ RELHARMVEC=[1]
...

The decade (DEC) sweep generates F_swept values of 1, 10, and 100. An input frequency is calculated for each swept value. In this example with one SS_TONES frequency, there is only one product:

(relharmvec[1] × SS_TONES[1]) = (1 × 1000) = 1000.

Then:

F_output[1] = 1 + 1000 = 1001

F_output[2] = 10 + 1000 = 1010

F_output[3] = 100 + 1000 = 1100

The default for RELHARMVEC is a vector of zeros; with this value, the output frequencies are just the swept frequencies.

For the gain calculation, Nexxim TV Noise computes the input frequency F_input at each of the values of the output frequency F_output by adding sum of the products of each of the (n) steady-state frequencies F_{SS_TONES} multiplied by the corresponding REFSIDEBAND coefficient:

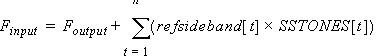
Here is a simplified example. This example uses a single output frequency.

.TV_NOISE
+ POI 1 1000000 // Single frequency for the sweep
+ SS_TONES=[1000, 2000, 3000]
+ RELHARMVEC=[0, 0, 0] // This is the default
+ REFSIDEBAND=[-1, 1, 2]

The resulting calculation would be:

SUM1 = (0 × 1000) + (0 × 2000) + (0 × 3000) = 0

F_output = F_swept + SUM1 = 1000000 + 0 = 1000000

SUM2 = (-1 × 1000) + (1 × 2000) + (2 × 3000) = 7000

F_input = F_output + SUM2 = 1000000 + 7000 = 107000

Typically, the sweep specification generates several output frequencies, perhaps using RELHARMVEC coefficients other than zero.

The Onoise output vector is calculated for the specified output devices at the output frequencies. Nexxim combines the harmonic frequencies (from -SS_MAXK to +SS_MAXK, plus 0) of each of the steady-state tones (specified by SS_TONES) with the output frequencies to calculate a vector of internal noise frequencies that can contribute to the Onoise output.

The formula is too complicated to write explicitly. Here is a numerical example.

.TV_NOISE
+ POI 1 1000000 // Single frequency for the sweep
+ SS_TONES=[1001, 20000]
+ RELHARMVEC=[0, 0] // This is the default
+ SS_MAXK=[1, 2]+

Using the default for RELHARMVEC, F_output is just the swept frequency, one megahertz.

The F_onoise vector is calculated for every combination of harmonics (-1, 0, +1) for the 1001-Hz steady-state tone and harmonics (-2, -1, 0, +1, +2) for the 20000-Hz steady state tone. The resulting vector would have (3 × 5) = 15 elements:

1000000 + (0 × 20000) + (0 × 1001) = 1000000
1000000 + (0 × 1001) + (1 × 20000) = 1020000
1000000 + (0 × 1001) + (2 × 20000) = 1040000
1000000 + (0 × 1001) + (-2 × 20000) = 960000
1000000 + (0 × 1001) + (-1 × 20000)= 980000
1000000 + (1 × 1001) + (0 × 20000) = 1001001
1000000 + (1 × 1001) + (1 × 20000) = 1021001
1000000 + (1 × 1001) + (2 × 20000) = 1041001
1000000 + (1 × 1001) + (-2 × 20000) = 961001
1000000 + (1 × 1001) + (-1 × 20000) = 981001
1000000 + (-1 × 1001) + (0 × 20000) = 998999
1000000 + (-1 × 1001) + (1 × 20000) = 1018999
1000000 + (-1 × 1001) + (2 × 20000) = 1038999
1000000 + (-1 × 1001) + (-2 × 20000) = 958999
1000000 + (-1 × 1001) + (-1 × 20000) = 978999

Nexxim then calculates the noise output at these frequencies.

Periodic Transfer Function Computation Formulas

The netlist must specify the combination of harmonics of the steady state SS_TONES frequencies, using either MAXSIDEBAND or SIDEBAND.

When the SS_TONES list has only one frequency, you can use the MAXSIDEBAND entry to specify the maximum harmonic of that frequency. The input frequencies will be calculated using the formula:

F_input = F_output + {-K × f1 to K × f1}

Where F_output is the output frequency (possibly swept), K is the value specified for MAXSIDEBANDS, and f1 is the frequency specified in the SS_TONES entry.

Alternatively, you can specify a set of specific sidebands to use for the single output frequency, using the SIDEBAND entry. For example, if the SS_TONES frequency is f1, the entry

SIDEBAND=[1,3,-5]

specifies a calculation of the input frequencies using the following set of frequencies:

F_input = F_output + {(1 × f1), (3 × f1), (− 5 × f1)}

When the SS_TONES list specifies more than one frequency, you must use the SIDEBAND entry to specify the combinations of harmonics that are of interest as input frequencies (MAXSIDEBANDS is not valid with multiple SS_TONES frequencies). Each combination of harmonic numbers (positive integers, negative integers, or zero) contains one value for each of the frequencies in the SS_TONES list. For example, if the SS_TONES list contains two frequencies f1 and f2, the entry

SIDEBAND=[1,0,2,-1,1,1]

specifies three combinations of harmonics of the two SS_TONES frequencies, and the input frequencies would be calculated using the formula:

F_input = F_output + {(1 × f1+ 0 × f2), (2 × f1- 1 × f2), (1 × f1+ 1 × f2)}

Floating Node Warning

Nexxim issues a warning message if the circuit contains floating nodes or nodes with single connections. Only nodes with a single branch connection that is both conservative and constitutive are flagged. For example, the controlling nodes in a VCVS have a constitutive/behavioral/relational connection to the controlled nodes, but not a physical/structural/conservative connection, and therefore are not flagged.

                HFSS视频教程                                      ADS视频教程                               CST视频教程                           Ansoft Designer 中文教程

      Copyright © 2006 - 2013   微波EDA网, All Rights Reserved    业务联系：mweda@163.com