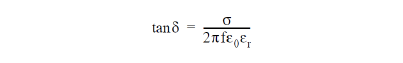
may be chosen so as to produce a dielectric with a given loss tangent at a particular frequency f according toIn CST MICROSTRIPES solid bodies can be formed from materials with a fixed, frequency independent relative permittivity and permeability and a fixed conductivity.
The conductivity may be chosen so as to produce a dielectric with a given loss tangent at a particular frequency f according to
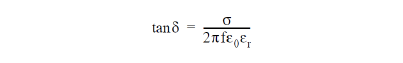
This may or may not give the desired loss tangent at other frequencies, and so may restrict the useful frequency range to a narrow band around 
. The CST MICROSTRIPES Build module allows the user to specify the conductivity by giving a frequency and the corresponding loss tangent.
The electric or magnetic polarizabilities of Debye materials exhibit simple poles. The permittivity or permeability of such a material steps down as the frequency is increased through each pole. The relative permittivity of an N-pole Debye material may be expressed as
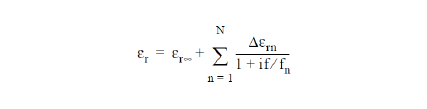
where er¥ is the relative permittivity at infinite frequency, Dern is the step in relative permittivity associated with the nth pole at frequency fn. The frequency of a pole is often expressed in terms of the corresponding
relaxation time
.
The polarizabilities of Lorentz materials have pairs of complex poles, and these materials may exhibit resonant absorption. The relative permittivity of a Lorentz material may be expressed as
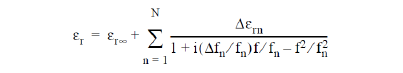
where Qn = fn / Dfn is used to characterise the degree of resonant behaviour.
In CST MICROSTRIPES a material may have any combination of simple (Debye) and paired (Lorentz) poles. Each pole may be associated with a step in the relative permittivity or permeability or both. Additionally, the material may have a fixed, frequency independent conductivity.
The material properties are specified by giving the zero-frequency properties and , and pole parameters. Specifying Qn = 0 gives a simple (Debye) pole, and otherwise paired (Lorentz) poles. Build allows the user the option of specifying the relaxation time rather than the frequency of a pole.
Note that the high frequency limit for the relative permittivity may not be less than one. Consequently, the low frequency limit must be at least one greater than the sum of the steps, i.e.
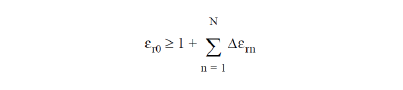
and similarly for the permeability.
In order that the user may check that the desired material responses are achieved, the 3D-TLM Simulator writes out the complex permittivity and permeability of each material as a function of frequency. This data is written to a file with the extension ‘.prop’ (for ‘properties’) which may be inspected with the graph plotter.
Each cell of frequency dependent material demands more computer memory and more run-time than a cell of simple material. This extra computational expense is proportional to the number of poles associated with the material - counting two for Lorentz poles, and counting electric and magnetic poles separately. Therefore, if there is a significant volume of frequency dependent material, it is worthwhile minimizing the number of poles considered. Poles significantly above the maximum frequency of interest should be neglected, while simple poles significantly below the minimum frequency of interest should be amalgamated with the d.c. conductivity. That is, each low frequency pole should be replaced by a contribution to the d.c. conductivity of
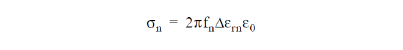
Anisotropic materials can only be modelled if the principle axes of the material are aligned with the coordinate axes.
Ideally, different dielectric bodies should not occupy the same volume and metal or thin panel bodies should not occupy the same surface. The 3D-TLM Simulator will check to see if ambiguous regions are included in the model if the tickbox ‘Allow different materials to overlap’ is unchecked on the Advanced dialog of the mesh definition dialog.
Metal bodies may always overlap dielectric bodies, in which case the region of overlap is taken to be metal. This is useful when metal parts are to be embedded in dielectric.