

 Signal
Signal New Excitation Signal
New Excitation Signal Signal type
Signal type
The stimulation is performed with a Gaussian pulse. To define a Gaussian-shaped excitation function a frequency range (Fmin, Fmax) must be specified.
This signal type is relevant in particular for high frequency calculations and is used there as default excitation function.
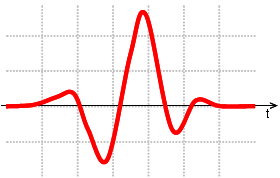
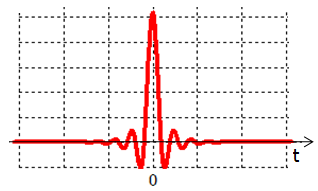
This excitation function is similar to the Gaussian pulse. However, it does not contain any DC part in its spectrum if Fmin is greater than zero.
If results at relatively low frequency are of interest choose the default Gaussian over this excitation function.
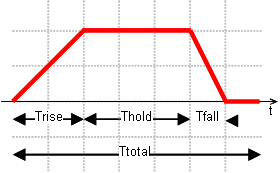
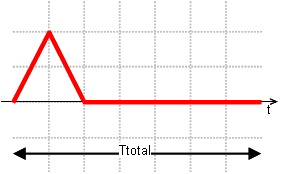
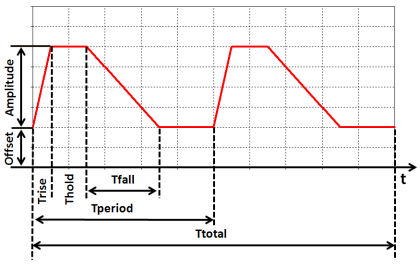
Enables you to define a digital excitation. Use Ttotal, Trise, Thold and Tfall to define the shape of the function. A step function can be obtained by setting Trise and Tfall to zero.
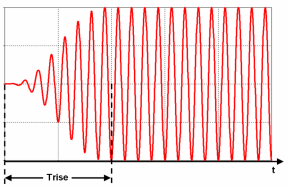
Enables you to define a sine step excitation. The parameters Frequency and Phase specify the parameters of the modulation with the sine function. The maximum Amplitude is reached after t=Trise.
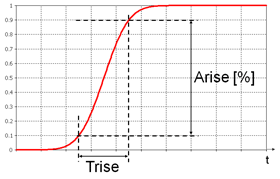
Enables you to define a smooth step excitation, whose amplitude grows from 0 (start) to 1 (end) amplitude. The parameters Trise and Arise [%] specify the slope of the signal, in term of its rise time and the amplitude (in per cent notation) rise interval. In the following picture, for instance, Arise=80%, denoting a growth interval between 10% - 90% value. The definition of the rise interval is always assumed symmetric with respect to 50% value. In a similar way a rise interval between 20% - 80% value is specified by Arise = 60%.
Enables you to define a double exponential excitation using the following expression.
f (t) = A (exp (-t / B) - exp (-t / C))
A: Amplitude
B: Tfall
C: Trise

Enables you to define an impulse excitation.
A highest required output frequency (Fmax) should be specified to define the shape of this signal.
This signal is centred about zero. It starts at t = -6.25 / Fmax and ends at 6.25 / Fmax. Outside this range, the signal is zero.
The edit button opens the VBA editor that lets you define an excitation function. Please note that the total time of a user defined signal is always interpreted in the unit seconds.
Example:
Option Explicit
Function ExcitationFunction(dtime As Double) As Double
If ( dtime < 1.0e-9) Then
ExcitationFunction = 1.0e9 * dtime
ElseIf ( dtime < 2.0e-9 ) Then
ExcitationFunction = -1.0e9 * dtime + 2
Else
ExcitationFunction = 0
End If
End Function
Enables you to import a two-column table from an ASCII file which contains the time and signal data. Please note that the data of an imported signal is always interpreted in the unit seconds.
Enables you to define a sine-shaped excitation. The parameters Voffset and Frequency specify the vertical offset of the sine function and the number of periods within one second (depending on the predefined frequency unit setting), respectively. After Ttotal time units the signal will fall to zero.

Enables you to define a Heavyside step excitation. The parameters Astart and Aend specify the amplitude values before and after t=0. At t=0 the function value is Astart.

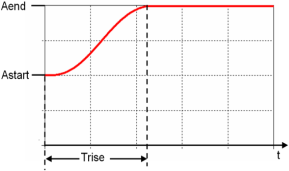
Enables you to define a polynomial step excitation. The parameters Astart and Aend specify the start and end amplitudes. The end amplitude is reached after t=Trise.
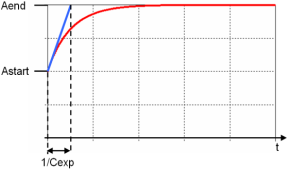
Enables you to define a exponential step excitation. The parameters Astart and Aend specify the start and end amplitudes. Cexp is the exponential constant which determines the functions gradient. At t=0 the gradient is: Cexp*(Aend-Astart)..
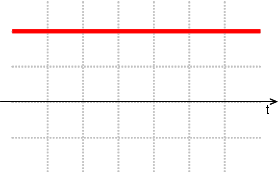
Yields the same constant value 1.0 for all time steps. This signal is used as default in low frequency calculations. It has no meaning for high frequency calculations.
The trapezoidal signal is a periodic function with an offset and a trapezoidal pulse whose amplitude is scaleable.
The definition is very similar to the one of the rectangular signal except that the offset and the amplitude is available in addition.
See also
Excitation Signal View, Excitation SignalExcitation Signal Library