

Introduction
In the field of numerical computations, there exists a class of problems, the solutions of which are difficult to obtain with common methods. Let us consider a simple example: a metallic ball, to the whole surface of which a constant normal pressure is applied. At first glance, the solution of this problem would be the same ball with its radius changed due to the homogeneous compression.
However, no displacement boundary conditions have been defined in this formulation. Thus, if any translation (or small rotation) of the ball were added to the solution, it would still satisfy the problem statement. Thus, any real-world solver would return a solution consisting of the following components:
The radius of the ball is changed due to the external pressure (scaling);
The ball is translated;
The ball is rotated.
The latter two components of the solution randomly depend on the discretization, rounding error etc. This is a classical example of an ill-posed problem. In order to stabilize the solution, additional constraints should be applied to it. This process is called regularization.
For the present example, a reasonable choice would be to select the solution with the minimal norm. This would reduce the unstable components to zero, keeping only the meaningful scaling component.
Method
The basic task of the structural mechanics solver is to build and solve the following matrix equation:
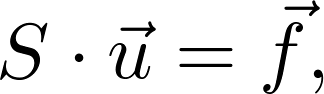
where S is the stiffness matrix, f the volume force density and u the unknown distribution of node displacements. In this case, regularization consists in the extension of this equation by a regularization term:
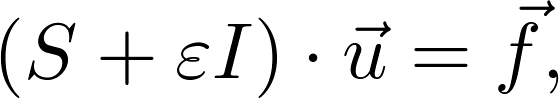
where I is the identity matrix and ɛ is the regularization parameter. This type of regularization is commonly referenced to as Tikhonov 0-order. The solution of this equation can be expressed as follows:
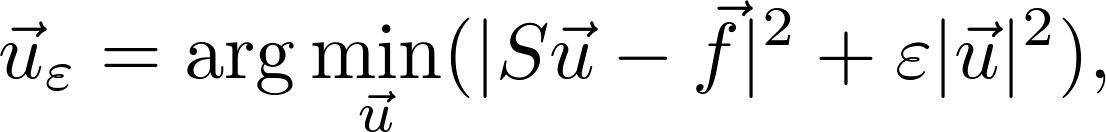
Thus, of all the possible distributions of node displacements, the one satisfying the initial problem and having the smallest Euclidian norm is selected.
It is worth mentioning, that the displacement in each point is defined by a vector in 3D space. Thus, it is possible to apply regularization only to the selected components of displacement, ignoring the rest of them.
User Interface
In the Mechanical Solver Specials dialog, you can select between three modi of regularization:
"None" means, that no regularization should be applied to the solution;
In the "Auto" mode, the solver looks through all the displacement boundary conditions and checks, which components of displacement are specified in none of them. Regularization is applied to only these components.
"Full" means, that regularization is applied to all three components of displacement.
See also