TDR (Time Domain Reflectometry)
Result Templates Template Based Post Processing Template Based Post Processing Time Signals Time Signals
This template evaluates the impedance profile along a TEM or similar
structure based on the reflected time signals at a port (mode).
TDR computation (Time Domain Reflection) is well known from measurement,
where TDR is the only possibility to 鈥漧ook into a structure鈥?and locate
mismatches. Typically TDR is applied to TEM structures such as connectors
or IC packages designed to have minimum return loss. CST MWS with its
transient solver is ideally suited for this task, since TDR pulses have
to be short in time (to be able to resolve discontinuities in space) and
thus extremely broadband.
The TDR can be calculated with two kind of excitations: 1)
step time signal or 2) Gaussian
time signal. The template automatically recognizes the signal type
and switches between the different TDR calculation methods 1) and 2):
1) Step time signal
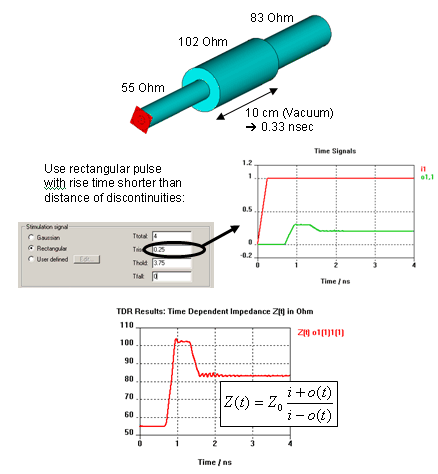
A rising
rectangular pulse as excitation signal is the typical pulse for TDR evaluation.
It has however the disadvantage, that the energy is not decaying (time
signal never stops) as well as that the frequency data such as S-Parameters
has some "undefined frequencies" due to zero-amplitudes in the
excitation spectrum. Both disadvantages do not appear when exciting with
a gaussian pulse. That's why using a gaussian pulse according to method
2) is recommended.
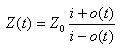
鈥漐(t)鈥?is the TDR impedance, 鈥漐0 鈥漣s the port line impedance, 鈥?i鈥?is
the amplitude of the input step signal. 鈥漮(t)鈥?is the reflection signal.
Note: In
order to resolve the stimulated highest frequencies in time and space
by the discretization, you should choose the upper frequency limit to
at least 1/Trise.
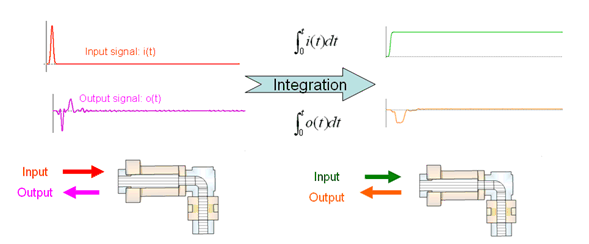
2) Gaussian time signal
When using a gaussian pulse, the TDR is
calculated from the time integral of the pulse, which again is the well-known
(smooth) step function.
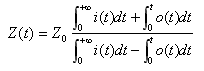
鈥漐(t)鈥?is the TDR impedance, 鈥漐0 鈥漣s the port line impedance, 鈥?i(t)鈥?
is input Gaussian signal . 鈥漮(t)鈥?is the reflection signal.
Note: The
rise time in this case correlates to the upper limit of the frequency
band. The frequency range should be adjusted to fmin=0, fmax=鈥?.876 /
rise time鈥? The rise time is the 10% to 90%
rising time of a corresponding step signal, which is the result of an
integrated gaussian pulse.
Example: if the rise time should be 35 ps, then fmax
= 0.876/35ps = 25.14GHz. You can see the Gaussian
pulse below. The integral of this pulse gives you the step signal with
35ps 10% to 90% rise time.
Gaussian Pulse options
This frame contains two options, which only apply to the Gaussian pulse.
Both options should not be used in case of a step type input signal.
Shift T_0(TDR) to T_50%(Pulse)
This option shifts the TDR response in time:
The TDR plot then starts at t=0, when the input pulse for the TDR computation
reached 50% of its maximum.
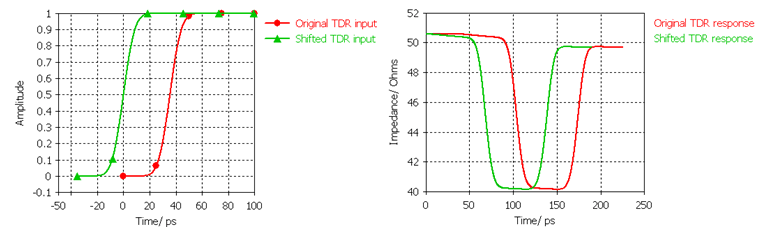
The pictures illustrate the shift in time,
when the Gaussian Pulse is used. For a step pulse, this can be done manually
using e.g. the 1D Result from 1D Result template.
The shift option is generally used in order
to avoid the time before the pulse and the return signal establishes.
This is most useful, if you want to compare the TDR to the measurement
or cross probe from the TDR to the device under test.
Note: When using the TDR from S-Parameters
calculation, the TDR is automatically shifted in time to comply with this
setting.
Calculate Reflection Factor
This option, when checked, calculates the
reflection factor over time instead of the time domain reflectometry (TDR).
The reflection factor is bound between -1 and +1. Therefore even for an
open transmission line, the reflection factor stays within these limits
鈥?in contrast to the TDR, which is infinite in this case. The reflection
factor is also useful, if the structure needs to be optimized, hence the
reflection minimized.
OK
This button completes the setup of the template.
The new entry will be added to the list of templates which are executed
automatically after each run. The default name of the template is set
according to the settings, as long the name has not been changed manually.
Cancel
Aborts the setup of the template and closes
this dialog box without performing any further action.
Help
Shows this help text.
See also
Preloaded
Result Templates, Preloaded
Macros Overview, Time
Signal Processing / Eye Diagram, Time
Signal Processing / Exchange Excitation




HFSS视频教程
ADS视频教程
CST视频教程
Ansoft Designer 中文教程
|
