The 3D-TLM simulator works in the time-domain. The duration of the simulation is the length of time simulated - it is proportional to the computer run-time.
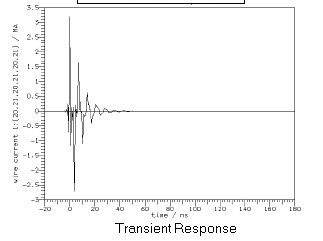
In the ideal case, the time-domain response of the model is transient, and the electromagnetic field decays to a negligible level after a short time. This situation can be recognized from the nature of the model. If the model is strongly coupled to matched terminations at its ports, if it radiates freely, or if it includes lossy materials, then the model will lose energy quickly and its time-domain response will be brief. An example of a transient response is shown below.

Once the response has decayed, it has essentially been captured by the simulation and there is nothing to be gained from continuing. A guess at how long this might take can be made from the size of the model (the electromagnetic field energy travels from its source to a point where it is absorbed or radiated away, at up to the speed of light.) The energy may then be partially reflected, so that it must traverse the model a number of times before decaying. Reflections at discontinuities within the model, and group velocities of less than will also tend to delay the energy’s decay. These considerations suggest that a duration of (say) twenty times the largest mesh dimension divided by the speed of light would generally be sufficient. This estimate must be increased for highly resonant structures, but may be reduced in many other cases, such as for antennas.
Rather than requiring the user to specify a number of nano-seconds, Build allows the duration to be specified in terms of the distance covered in that time by light in free space.
Build sets a sensible default duration. However, the user should ensure that Duration: time as distance (time ´ c) is set to several times the largest mesh dimension
CST MICROSTRIPES can display a graph of the time-domain response which is updated as the simulation proceeds. Whether or not this facility is used, it is possible to interrupt the 3D-TLM simulator at any point and request that the response so far is written out (along with any other output). If the user considers the response sufficiently complete, then the simulation can be terminated.
In certain circumstances, it is preferable to specify a longer duration than default. This gives the user the option to stop the simulation at a time when the energy has sufficiently decayed. It is not possible to re-start a simulation from the point of termination.
Since it is not possible to run a simulation for an infinite time, the time-domain signal from the simulator must be truncated at some point. This is equivalent to multiplying the infinite time-domain response by a long square pulse of unit height, and length equal to the simulation duration .
By the convolution theorem, the effect on the frequency domain response is to convolve it with the Fourier transform of this pulse, i.e. to convolve it with or or to within a phase factor with times "". (The phase factor appears because the pulse is not centered on ). The Fourier transform of such a pulse or window is shown below.
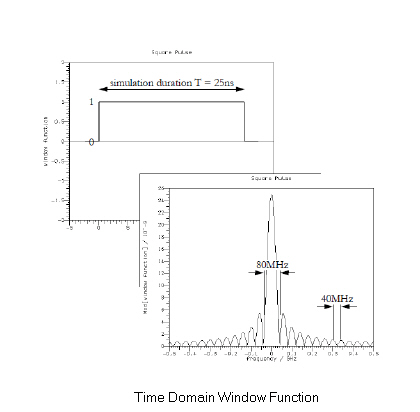
Next we consider the effects of convolving our frequency domain response with this function.
In the example shown below, the time-domain response has been cut short after 25ns - at which point the response has not decayed, there remaining a strong 1ns-period (1GHz) oscillation
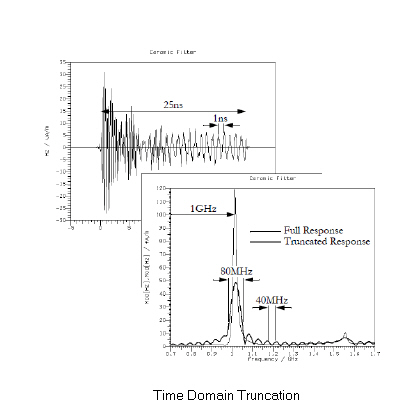
Three effects of the truncation are visible in the frequency domain:
• The 1GHz resonance has not attained its full height.
• There is a ripple of period 40MHz (i.e. 1/(25ns)) - almost obscuring the resonance at 1.55GHz.
• The resonance has an exaggerated width of 80MHz (i.e. 2/(25ns))
For a simulation of duration , these effects will make it impossible to resolve features of the frequency domain response which are closer together than about . Furthermore, the ripple will introduce a small uncertainty into the frequency of any resonance. The ripple will also be apparent in any frequency domain parameters derived from the simulation - the elements of a scattering matrix for example.
Many microwave devices incorporate resonant structures - such as cavities - which give rise to a very protracted time domain response. To simulate such a device until all the resonances have decayed can be time-consuming. To circumvent this difficulty, CST MICROSTRIPES provides a Predict facility which takes an incomplete (filtered) time domain response and attempts to extend it to later times by linear prediction.
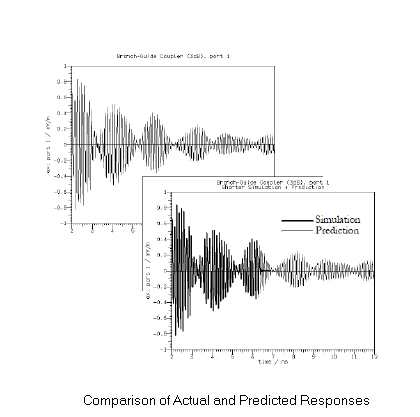
Essentially, the method first identifies the resonances, their frequencies and rates of decay and then decomposes the signal at each output point in the device into a (different) linear combination of these resonances. This allows the response to be calculated at any future time, or at least until uncertainties in the resonances make the prediction unreliable
Of course, any linear system when it is not being driven by active sources has a response which is the sum of a number of damped sinusoids. However, the number of sinusoids which may be present is about half the number of degrees of freedom in the system. Even in a spatially discrete, finite volume TLM model this number could easily exceed 1 million. Most of these sinusoids will be transient - decaying very rapidly, or may be removed by low-pass filtering. When only some tens of resonances persist, it becomes feasible to discern each one individually, and for the Predict module to extrapolate the response.